24秋机器学习笔记-08-树模型与集成学习

本文主要涉及机器学习中的树模型以及集成学习。
一键回城。

树模型

决策树

回忆：我们之前的很多模型都可以写成 $y = w^Tx+b$，决策逻辑（二分类）：$f(x)\ge0$ 时预测为 $1$，否则预测为 $0$。

事实上这个逻辑可以写成一个树。

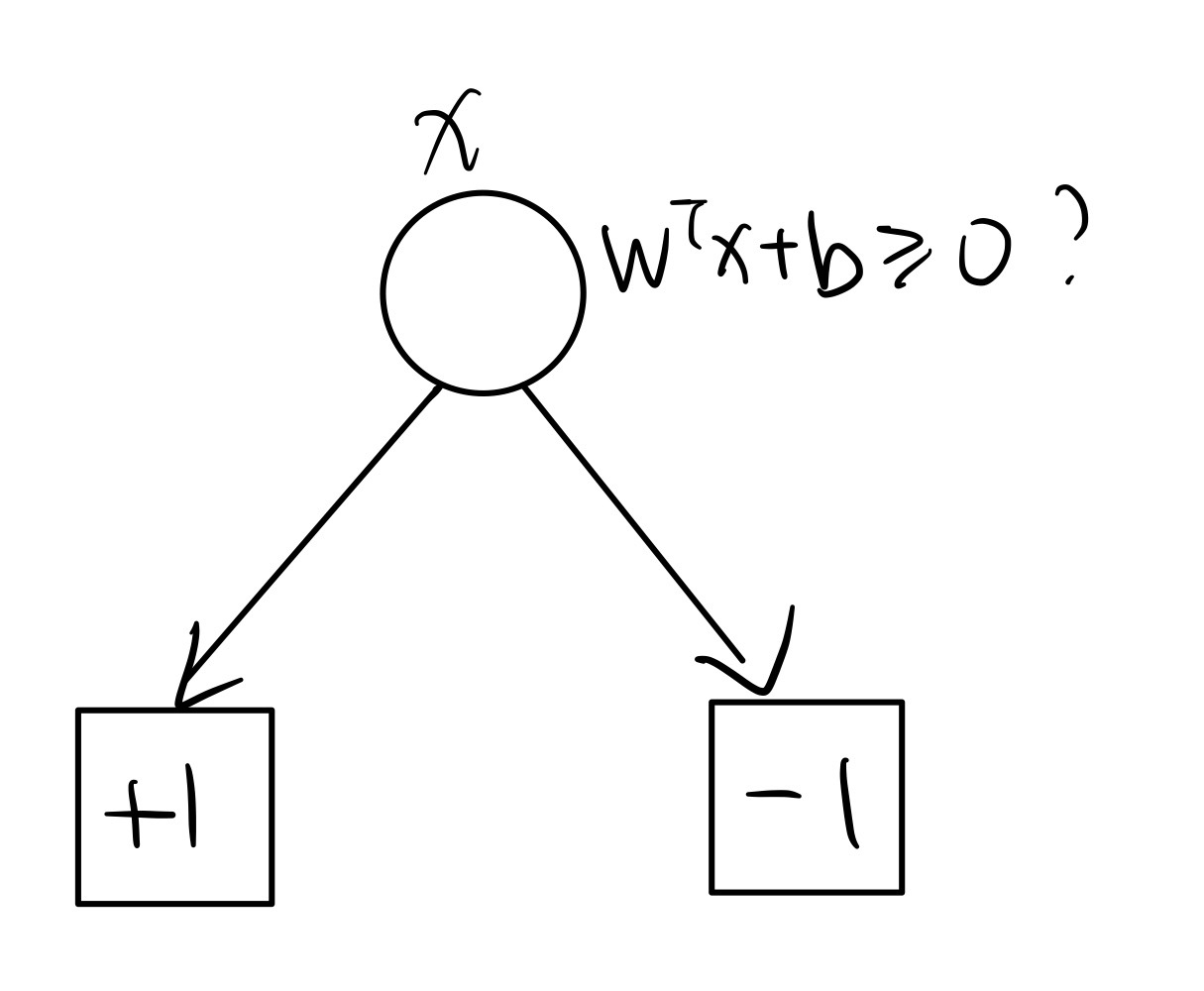
我们之前学习的模型多为线性模型，为了应对非线性性，我们可以考虑引入决策树。

决策树定义：一棵包含根节点、内部节点、叶子节点和有向边的树，每个非叶节点会将数据根据某种特性进行划分，一个数据点的预测值即为其对应的叶子节点对应的标签。

An example:

$y \in \{-1,+1\}$，$+1$ 表示其为一个好的研究者，$-1$ 表示其为一个不好的研究者。

收集的数据如下：

ID	A	B	C	y
1	√	√	√	$+1$
2	√	√	×	$+1$
3	√	×	√	$-1$
4	×	×	×	$-1$
5	×	√	×	$-1$
6	×	×	√	$-1$
7	×	√	×	$-1$
8	√	×	√	$-1$
9	×	√	×	$-1$

A 表示是否勤奋，B 表示是否有好的视野，C 表示是否喜欢吃香蕉（？）

一个可能的决策树如下：

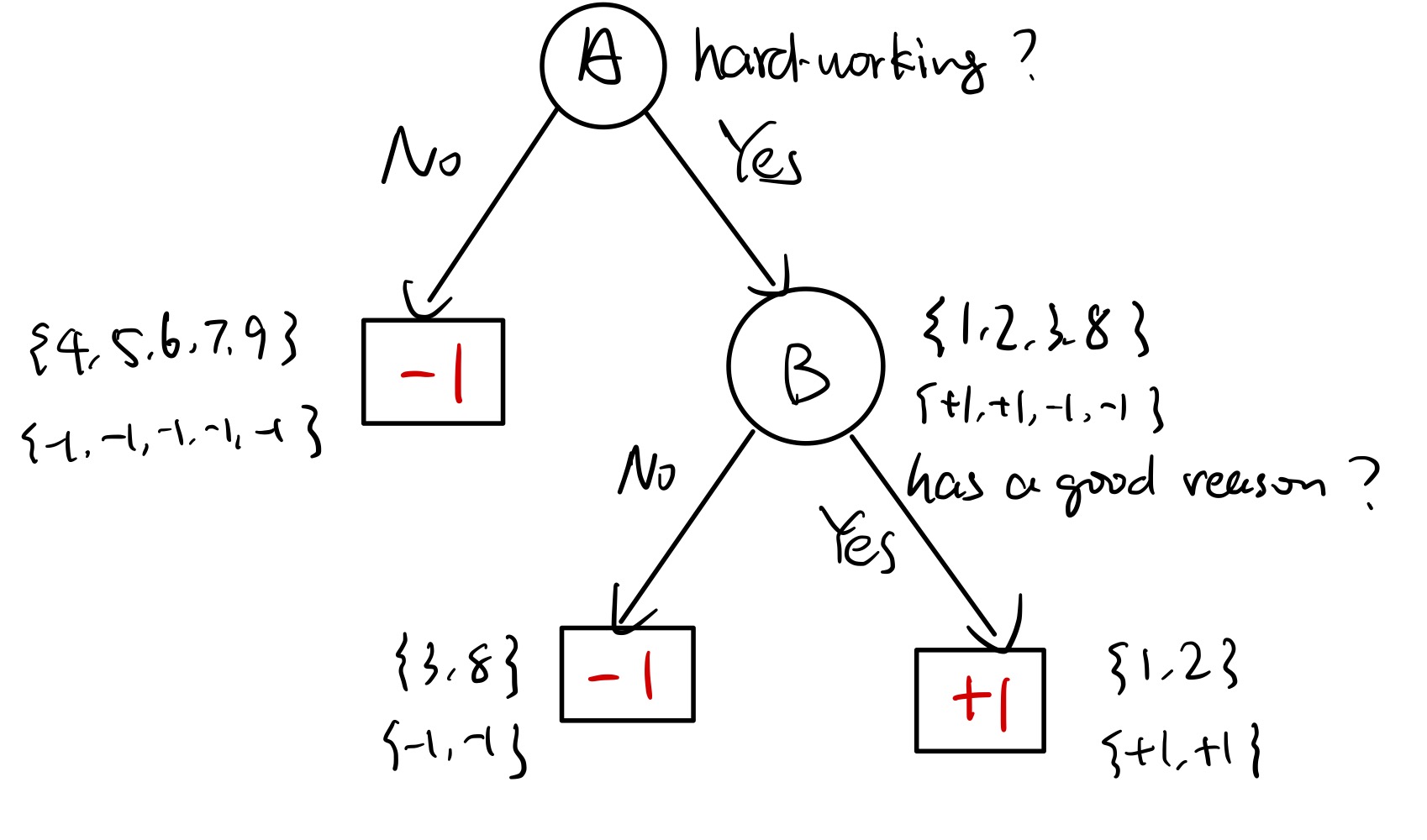
如果给定了一个十号数据点，$\{√,√,×\}$，用该决策树对其进行预测，则可得到结果为 $+1$。

但是如果用 C 特征呢？会发现划分出来的东西不是很纯

熵

如何进行数据的划分？一个好的划分准则应当尽可能纯地进行划分数据。但是现实中如上面一般简洁的例子是不太可能存在的，所以我们需要定量地进行研究。

“纯度“的反义词就是“混乱程度”，自然想到用熵去进行度量。

对于离散随机变量 $X$，其熵被定义为

$$H(X)= \sum_x p(x) \log \frac{1}{p(x)} = -\sum_x p(x)\log p(x)$$

此处 $\log$ 以 $2$ 为底数，熵的单位为 bits。考虑扔 $3$ 次硬币，硬币均匀，$X$ 表示结果。$H(X)=3$，对应我们需要用 $3$ 个 bits 来描述结果。但如果第三个硬币永远是正面，此时 $H(X)=2$，也就不需要第三个 bit 来编码第三个硬币了。

对于一个事件 $X = x$，$p(x)$ 越低，其“包含的信息量”越高，我们就用的是 $\displaystyle \log \frac{1}{p(x)}$ 表示所谓的“信息量”。例如，$x=$“太阳在东方升起”，$p(x)=1$，“包含的信息量极低”。又例如，$x=$“掷一个均匀骰子 $3$ 次，得到三个 $6$”，$\displaystyle p(x) = \left( \frac{1}{6} \right)^3 $，$\displaystyle \log \frac{1}{p(x)} \approx 7.75 \gg 0$，说明其“信息量”高，这是合理的。

而这个 $H(X)$ 衡量的就是所有事件的平均“信息量”，所以对 $\displaystyle \log \frac{1}{p(x)}$ 求期望也是不难理解的了。即衡量系统的不确定性，或者说混乱程度。

性质：

• 下界：$H(X)\ge 0$ 恒成立。显然。当 $\exists x$ 使得 $p(x)=1$ 时，等号成立。
• 上界：$\displaystyle H(X)\le \log\left( \sum_x p(x) \frac{1}{p(x)} \right) = \log n$，该上界由琴生不等式得到，考虑 $\log$ 的凹性（concavity）。等号当且仅当 $\forall x,p(x) \displaystyle =\frac{1}{n}$，这也是很符合直觉的。

条件熵与互信息

对于两个随机变量 $X,Y$，可以定义其互信息（mutual information）

$$I(X;Y) = H(Y) - H(Y\mid X)$$

$H(Y\mid X)$ 为条件熵（conditional entropy），意为观测到 $X$ 后 $Y$ 的不确定度。这里假设 $x$ 有 $m$ 种可能取值。

$$H(Y\mid X) = \sum_{i \in [m]}P(X=x_i) H(Y\mid X=x_i)$$

而 $I(X;Y)$ 衡量的就是某种观察到 $X$ 后，$Y$ 的不确定度的减少程度，也可以理解为 $X$ 中与 $Y$ 有关的信息量。

$X$ 与 $Y$ 越相关，$I(X;Y)$ 越大。其关系可以大致用如下的图表示：

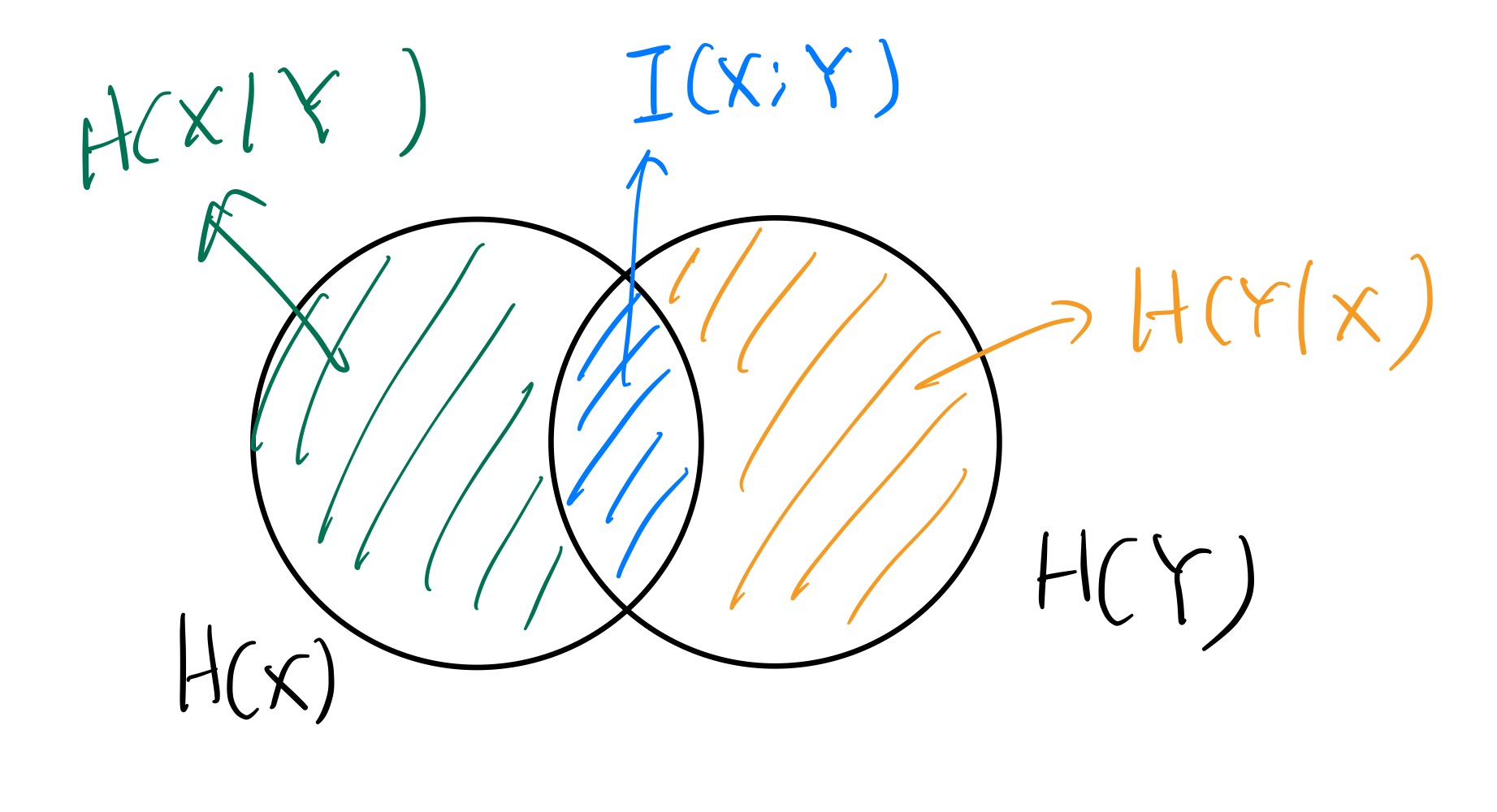
事实上可以发现，$I(X;Y)$ 具有对称性，即 $I(X;Y) = H(Y) - H(Y\mid X) = H(X) - H(X\mid Y)$。且 $I(X;Y) = H(X)+H(Y) - H(X,Y)$。

以及，当 $X,Y$ 独立时，$I(X;Y) = 0$，这是很符合直觉的。

信息增益（Information Gain）

信息增益（information gain）被定义为

$$g(D,A) = H(D) - H(D\mid A)$$

记号约定：$D$ 为训练集，$A$ 为某种属性（假设其为离散的，$A \in \{a_1, \cdots ,a_m\}$，有 $m$ 种离散取值），且假设问题为多分类问题，即 $y \in [K]$。

$H(D)$ 表示还未划分前，训练集中标签的纯度，定义为

$$H(D) = -\sum_{k \in [K]} \frac{|C_k|}{|D|} \log \frac{|C_k|}{|D|}$$

其中 $C_k$ 表示 $D$ 中标签为 $k$ 的数据构成的子集，$\displaystyle \frac{|C_k|}{|D|}$ 事实上就是在衡量 $P(y = k)$。

$H(D\mid A)$ 定义为

$$\begin{aligned} H(D\mid A) &= \sum_{i \in [m]} \frac{|D_i|}{|D|}\cdot H(D\mid A = a_i) \\ &= -\sum_{i \in [m]} \frac{|D_i|}{|D|} \sum_{k \in [K]} \frac{|D_i \cap C_k|}{|D_i|} \log \frac{|D_i \cap C_k|}{|D_i|} \end{aligned}$$

$D_i$ 表示 $D$ 中满足 $A=a_i$ 的数据构成的子集，$\displaystyle \frac{|D_i \cap C_k|}{|D_i|}$ 就是在度量 $P(y = k\mid A =a_i)$。

$g(D,A)$ 就表示的是，用 $A$ 划分 $D$ 后，能使得混乱程度减少多少，即 $\displaystyle A^* = \argmax_A g(D,A)$。

结合前面的条件熵相关知识，我们发现 $g(D,A)$ 的本质就是 $H(y) - H(y\mid A) = I(y;A)$，要选择一个与 $y$ 的互信息最大的 $A$，这也是很符合直觉的。

例：假设有特征 $A,B$，$A$ 有两个离散等概率取值 $a_1,a_2$，$B$ 有十个离散等概率取值 $b_1,\cdots,b_{10}$，分类标签 $y \in [10]$ 且在数据集 $D$ 内均匀分布。假设 $y$ 在每个 $b_i$ 下是“纯的”，且 $A=a_1 \implies y \le 5,A=a_2\implies y \ge 6$（也各自是等概率的，即 $\displaystyle P(y=i\mid A=a_1) = \frac{1}{5}, \forall i \in [5]$，$a_2$ 的情况同理），计算 $g(D,A)$ 与 $g(D,B)$。

首先，$\displaystyle P(A=a_i) = \frac{1}{2},P(B = b_i) = \frac{1}{10}$。

$$H(D\mid A=a_1) = -\sum_{i \in [5]} \frac{1}{5} \log \frac{1}{5} = \log 5\\ H(D\mid A=a_2) = \log_5$$

所以，$H(D\mid A) = \displaystyle \frac{1}{2}\log 5 + \frac{1}{2} \log 5 = \log 5$

接下来，由于 $y$ 在每个 $b_i$ 中是纯的，所以 $H(D\mid B = b_i) = 0$，自然 $H(D\mid B) = 0$。

而 $H(D) = \log 10$（由等概率性）。所以 $g(D,A) = H(D) - H(D\mid A) = \log 2 = 1$，$g(D,B) = H(D) - H(D\mid B) = \log 10$。

自然，根据信息增益越大越好的准则，$\log 10>1$，我们应该选择 $B$ 来进行划分。

不过，这样的 $B$ 未必就是最好的。考虑以数据的 ID 为特征，一样能够做到在每个 $b_i$ 中都是纯的！ 或者说，每个样本都有一个自己的 feature，但这样的 $B$ 不具有泛化性，不能帮助我们做预测。这便是信息增益的一个巨大局限：更倾向于选择有很多 values 的 feature，但这样的 feature 未必是好的。

增益率（Information Gain Ratio）

定义：

$$g_R(D,A) = \frac{g(D,A)}{H_A(D)}$$

其中

$$H_A(D) = -\sum_{i \in [m]} \frac{|D_i|}{|D|}\log \frac{|D_i|}{|D|}$$

本质上就是 $H(A)$，衡量的是 $A$ 本身的混乱程度，$g_R(D,A)$ 相当于用 $H(A)$ 来“normalize” $g(D,A)$，可以“抵消” IG 对取值很多的 feature 的偏好性。

在刚才的例子中，继续计算 $g_R(D,A)$ 和 $g_R(D,B)$。由于 $A$ 和 $B$ 都是均匀的，所以 $H_A(D) = \log 2$，$H_B(D) = \log 10$。于是

$$\begin{aligned} g_R(D,A) &= \frac{g(D,A)}{H_A(D)} = \frac{1}{\log 2} = 1 \\ g_R(D,B) &= \frac{g(D,B)}{H_B(D)} = \frac{\log 10}{\log 10} = 1 \end{aligned}$$

在这个指标下，就不会更偏好于 $B$ 了。

基尼系数（Gini Index）

定义：

$$\operatorname{Gini}(D) = \sum_{k \in [K]} \frac{|C_k|}{|D|}\left( 1 - \frac{|C_k|}{|D|} \right)$$

可以理解为是在计算 $\displaystyle \sum_{k \in [K]} P(y = k)(1 - P(y=k))$，对比熵的定义 $\displaystyle \sum_{k \in [K]} P(y=k) \log \frac{1}{P(y=k)}$。趋势是一样的，所以基尼系数也可以理解为是在描述体系的混乱程度，基尼系数越大，不确定性越大。

接下来定义

$$\operatorname{Gini}(D,A) = \sum_{i \in [m]} \frac{|D_i|}{|D|}\operatorname{Gini}(D_i)$$

即，对于每个特征 $a_i$，分别计算每个划分下的基尼系数然后求平均。描述的是经过 $A$ 划分后的混乱程度。

其自然是越小越好的（注意和前面的 IG 和 IGR 不一样），即 $A^* = \displaystyle \argmin_A\operatorname{Gini}(D,A)$。

树回归

刚才我们一直在做分类问题。考虑当特征标签是连续的情况，即此时若我们是在做回归问题，如何衡量混乱程度？直接使用 L2 损失函数。

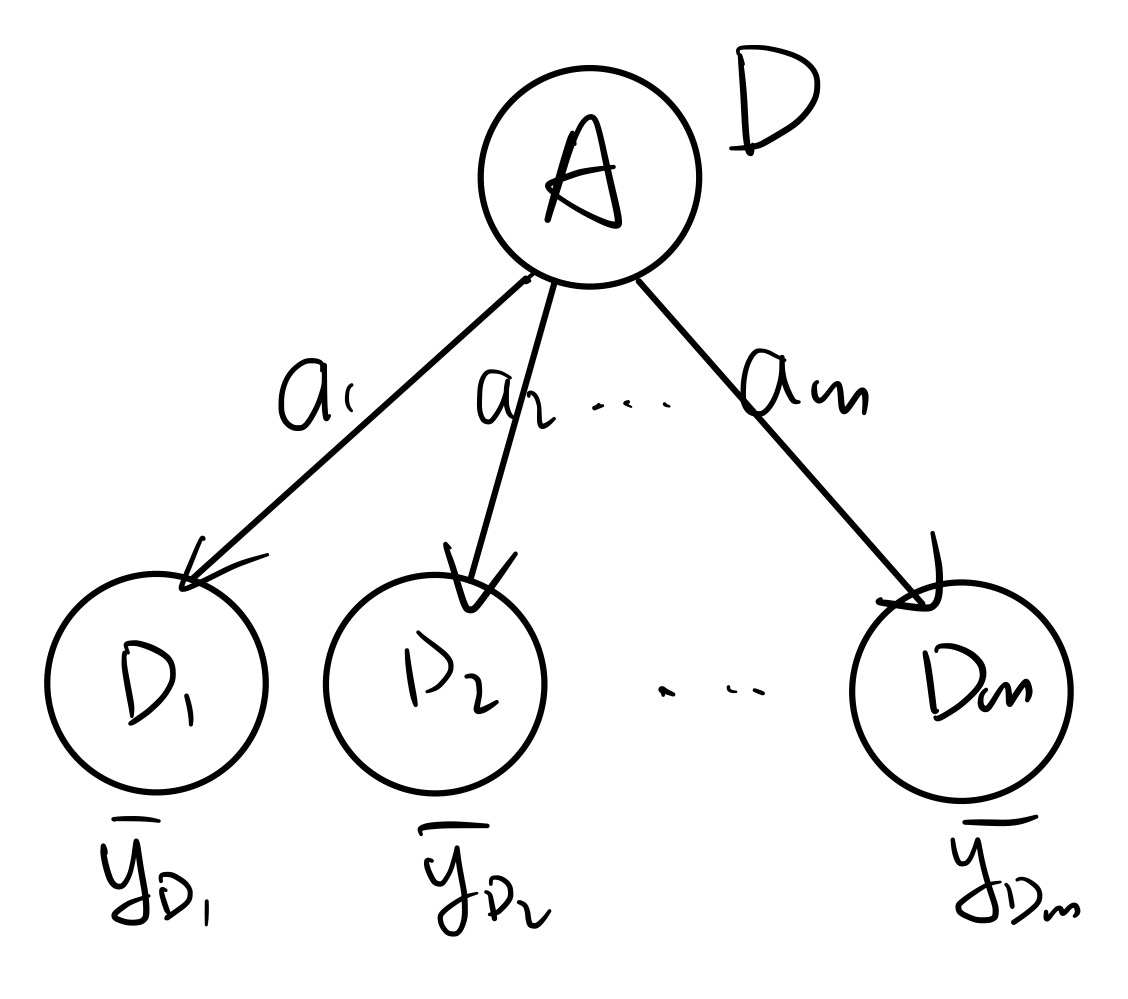
考虑上图的情况，特征 $A$ 有 $m$ 种取值，将 $D$ 划分为 $D_1,\cdots, D_m$。每一类内包含若干 $y$ 值。可以定义每一类内 $y$ 的平均值：

$$\overline{y_{D_i}} := \frac{1}{|D_i|} \sum_{j \in D_i} y_i$$

则可定义出损失函数

$$L(D,A) = \sum_{i \in [m]} \sum_{j \in D_i} (y_i - \overline{y_{D_i}})^2$$

选择特征时，即选择 $A^* = \displaystyle \argmin_A L(D,A)$。

决策树的构建

如果硬要考虑每种可能的顺序的话，构建决策树是一个 NPC 问题。所以一般而言使用贪心算法去进行决策树的构建。

即递归地，从根节点开始，选择一个最好的特征 $B$，进行划分，然后在每个子节点内重复如上过程（不能再用 $B$ 了）。

集成学习

Bagging (Bootstrap Aggregating)