24秋机器学习笔记-04-支持向量机（SVM）

本文主要涉及支持向量机（Support Vector Machine）以及对偶理论。
一键回城。
本文所涉及部分用了 3 个课时来讲述，内容较多。

带约束的优化问题

先介绍一般性的优化问题，进而引出 K.K.T 条件。

等式约束下的优化问题

$\min_x f(x)$，s. t. $h(x)=0$，其中 $f,h$ 都可微。

1. $\forall x$ 在平面 $h(x) = 0$ 上，有 $\nabla h(x)$ 与平面正交。
   如果有切向分量，说明我们沿着切向走可以使得 $h(x)>0$，与 $h(x)=0$ 矛盾。
2. 对于一个局部最小值 $x^*$，梯度 $\nabla f(x^*)$ 也与平面垂直。
   若有切向分量，则沿着其反方向走，可以保证 $h(x)=0$ 的约束不变，且 $f$ 可以继续降低。

一般而言，$x^*$ 为局部最小值的必要条件为：$\exists \lambda$ 使得 $\nabla f(x^*) + \lambda \nabla h(x^*) = 0$，即这两个梯度共线；以及 $h(x^*) = 0$。

不考虑 corner cases（事实上在实际中也少见）：我们需要 $x^*$ 为 regular point。

引入拉格朗日方程

$$L(x,\lambda) = f(x) + \lambda h(x)$$

其中 $\lambda$ 为拉格朗日乘子。

如果有多个约束，则

$$L(x,[\lambda_1, \cdots ,\lambda_n]) = f(x) + \sum_{i \in [n]} \lambda_i h_i(x)$$

此时，$x^*$ 为局部最小值的必要条件可以写为：$\exists \lambda$ 使得

$$\begin{cases} \nabla_x L(x^*, \lambda) = 0 \\ \nabla_{\lambda} L(x^*, \lambda) = 0 \end{cases}$$

第一个式子等价于 $\nabla f(x^*) + \lambda \nabla h(x^*) = 0$，第二个等价于 $h(x^*) = 0$。

无限制优化的时候，我们其实只需要 $\nabla f(x^*) = 0$，加上了约束之后，我们就利用拉格朗日乘子把约束放进方程里面。

同时，需要留意的是，如上为必要条件而非充分条件。

• 从拉格朗日条件解出来的解可能不是局部最小解
• 但是，所有的局部最小解肯定在我们解出来的 candidate set 里面。
• 对于凸函数，局部最小解即为全局最小解。

带不等式约束的优化问题

问题描述：$\min_x f(x)$ s. t. $g(x)\le 0$。

1. 同样地，对于任意在 $g(x)=0$ 平面上的 $x$，也一定有 $\nabla g(x)$ 垂直于平面，并且指向平面外。
2. 对于一个局部最优解 $x^*$：
   • 若其在平面上，则 $-\nabla f(x^*)$ 的方向必须与 $\nabla g(x^*)$ 相同。

     该条件等价于 $\exists \mu > 0$，s. t. $\nabla f(x^*)+ \mu \nabla g(x^*)= 0$。

   • 若在内部，已经满足约束 $g(x)\le 0$，则只需要满足 $\nabla f(x^*) = 0$ 即可。

     该条件等价于 $\exists \mu = 0$，s. t. $\lambda f(x^*) + \mu \nabla g(x^*) = 0$。（为了跟上面凑成一样的形式）

   • 所以，可以归结成：
     • $g(x^*) \le 0$；
     • $\mu \ge 0$；
     • $\mu g(x^*) = 0$（若 $g(x)$ 的约束 active，则 $g(x) = 0,\mu>0$，若 inactive，则 $g(x)<0,\mu = 0$）
     • $\nabla f(x^*) + \mu \nabla g(x^*) = 0$
   • 这四个条件称为 Karush-Kuhn-Tucker (KKT) 条件，为必要条件。

对其也可以定义拉格朗日方程：

$$L(x,\mu) = f(x) + \mu g(x)$$

KKT 条件说明，若 $x^*$ 为局部最小值，则：

• $\nabla_x L(x^*, \mu) = \nabla f(x^*) + \mu \nabla g(x^*) = 0$；
• $g(x^*) \le 0$；
• $\mu \ge 0$；
• $\mu g(x^*) = 0$。

等式/不等式约束都有的优化问题

问题描述：$\min_x f(x)$ s. t. $h_i(x) = 0, \forall i \in [k]$，$g_j(x) \le 0, \forall j \in [l]$

拉格朗日函数（其中 $\lambda,\mu$ 分别为 $k,l$ 维向量）：

$$L(x, \lambda, \mu) = f(x) + \sum_{i \in [k]} \lambda_i h_i(x) + \sum_{j \in [l]} \mu_j g_j(x)$$

其 KKT 条件：若 $x^*$ 为局部最小值，则必要条件为：

• $\nabla_x L(x^*, \lambda, \mu) = 0$（导数条件）；
• $\forall i \in [k]$ 有 $h_i(x^*) = 0$ 以及 $\forall j \in [l]$ 有 $g_j(x^*) \le 0$（可行性条件）；
• $\forall j \in [l]$ 有 $\mu_j \ge 0$；
• $\forall j \in [l]$ 有 $\mu_j g_j(x^*) = 0$（互补松弛条件）。

还是有不等式条件，所以不一定能从 KKT 条件直接求出 candidate solutions。

SVM 原始形式推导

SVM 是一个线性分类器：$f(x) = w^Tx + b$，$y \in \{-1,1\}$（同样只是 index）。

回忆：数据点线性可分的时候逻辑回归无穷多解的情况。

SVM 有一个明确的准则选择“最好的”分隔超平面：寻找一个使得间隔（margin）最大的超平面。margin 被定义为数据点到超平面的最小距离（max-min problem）。思想为结构风险最小化（Structural Risk Minimization）

Margin 越大，泛化性越强，也对离群值（outliers）更健壮（robust）。

而且一定在超平面两边都有至少一个（可以用调整法证明）能够支持这个超平面的点（称为 Support Vectors）

注意到，支持向量是直接决定分隔超平面的，但其他的点完全不会对支持向量的决策产生任何影响（对应表达式中的 inactive 约束）。

显然，$x_i$ 到超平面的距离为

$$d_i = \frac{|w^Tx+b|}{\left\| w \right\|}$$

推导？考虑垂足 $x_0$，则可以有

$$\begin{cases} x_0+d_i\cdot \frac{w}{\left\| w \right\|} = x_i \\ w^Tx_0 + b = 0 \end{cases}$$

注意这里的 $d_i$ 带有方向的含义，我们改用 $\gamma_i$ 表示。上式左乘 $w^T$ 即可配凑出 $w^Tx_0$，可以用 $-b$ 换掉，于是即推出

$$\gamma_i = \frac{w^T x_i+b}{\left\| w \right\|}$$

取绝对值即得到 $d_i$ 的式子。

也可以用拉格朗日乘子法。

相当于我们需要 $\displaystyle \min_{x_0} \frac{1}{2} \left\| x_i - x_0 \right\|^2$ s. t. $w^Tx_0 + b = 0$。

写出拉格朗日方程：

$$L(x_0,\lambda) = \frac{1}{2}\left\| x_i - x_0 \right\|^2 + \lambda (w^Tx+b)$$

求偏导有

$$\begin{cases} -(x_i - x_0) + \lambda w = 0\\ w^Tx_0 + b = 0 \end{cases}$$

类似地，上式左乘 $w^T$ 可以解得 $\displaystyle \lambda = \frac{w^T x_i + b}{\left\| w \right\|^2}$

回代，$\left\| x_i - x_0 \right\| = |\lambda| \left\| w \right\| = \displaystyle \frac{|w^T x_i + b|}{\left\| w \right\|}$，与前面得到的结果一致。

事实上我们会更多关注 $\gamma_i$，因其带有方向信息。$\gamma_i>0$ 代表点 $x_i$ 在 $w^Tx+b>0$ 区域内，反之亦然。

定义

$$\bar{\gamma_i} = y_i \gamma_i = \frac{y_i(w^T x_i + b)}{\left\| w \right\|}$$

可以通过 $\bar{\gamma_i}$ 是否大于 $0$ 判断一个点是否被正确分类（这里体现出一开始我们规定 $y_i \in \{-1,1\}$ 的好处），就不需要分类讨论正负类的 $\gamma_i$ 大于还是小于 $0$ 了。

而之前讨论的所谓 margin 就是

$$\gamma = \min_{i \in [n]} \bar{\gamma_i}$$

于是，我们之前说过的优化问题就变为：$\displaystyle \max_{w,b} \gamma$ s. t. $\forall i \in [n]$ 有 $\bar{\gamma_i} \ge \gamma$。

约束条件改写一下，变为：$\displaystyle \frac{y_i(w^Tx_i + b)}{\left\| w \right\|}\ge \gamma$。

对于支持向量们，一定有 $\bar{\gamma_i} = \gamma$。假设 $x_0$ 是某个支持向量，则 $\displaystyle \frac{y_0(w^Tx_0 + b)}{\left\| w \right\|} = \gamma$，用该式子替换掉 $\gamma$，优化问题变为 $\displaystyle \max_{w,b} \frac{y_0(w^Tx_0+b)}{\left\| w \right\|}$ s. t. $\displaystyle y_i(w^T x_i+b)\ge y_0(w^Tx_0+b)$。

称 $y_0(w^Tx_0+b)$ 为 functional margin，$w,b$ 可以任意缩放使得其任意大或任意小（但这不影响 geometric margin）。

所以还不如直接令 $y_0(x^Tx_0+b) = 1$，某种程度上是种正则化。

所以优化的表达式变为 $\displaystyle \max_{w,b} = \frac{1}{\left\| w \right\|}$ s. t. $\forall i \in [n]$ 有 $y_i(w^T x_i + b)\ge 1$。等价于 $\displaystyle \min_{w,b} \frac{1}{2} \left\| w \right\|^{2}$（该形式更方便进行求导），该形式称为 SVM 的原始形式（The Primal Form of SVM）

该形式强制令 functional margin = 1，$y_i(w^T x_i+b)\ge 1$ 而不是 $\ge 0$ 可以理解为要求所有的点到平面都有一个距离，以保证结构鲁棒性。

注意到这是一个二次规划（Quadratic Programming），有很多现成的标准包可以进行解决，具体的解决方法不在本节课的范围内。

剩余两个未能解决的问题：

• 不线性可分
• 线性可分但是有使得 margin 过于小的 outlier

SVM 对偶形式（Dual Form of SVM）

考虑拉格朗日函数（习惯上用 $\alpha$ 而不是之前的 $\mu$）

$$L(w,b,\alpha) = \frac{1}{2}\left\| w \right\|^{2}+\sum_{i \in [n]} \alpha_i(1 - y_i(w^T x_i + b))$$

定义

$$p^* = \min_{w,b} \max_{\alpha_i \ge 0} L(w,b, \alpha)$$

Claim：$p^*$ 为 SVM 主形式的一个解。

相当于我们将带约束的 SVM 主形式变成了不带约束的双层优化问题。

证明：假设某些约束没有被满足，则 $\exists i$ 使得 $1 - y_i(w^T x_i +b) > 0$，则里层优化会让 $\alpha_i \to +\infty$ 进而使得 $\displaystyle \max_{\alpha_i\ge 0}L(w,b,\alpha)\to +\infty$，所以外层的优化一定会让所有约束得到满足进而避免这种趋于正无穷的情况。

而里层的优化会使得 $\alpha_i = 0$，所以最外层优化的就是我们需要的解。

这个形式可能不太好解，所以把他转换为对偶形式：

$$d^* = \max_{\alpha_i\ge 0}\min_{w,b} L(w,b,\alpha)$$

弱对偶定理：$d^*\le p^*$。

证明：注意到 $\displaystyle \min_{w,b}L(w,b,\alpha)\le L(w,b,\alpha),\forall w,b$，即 $\displaystyle d^*\le \max_{a_i\ge 0}L(w,b,\alpha),\forall w,b$。所以 $\displaystyle d^*\le \min_{w,b}\max_{\alpha_i\ge 0}L(w,b,\alpha) = p^*$。

可以理解为两个人的博弈。最小的里面挑一个最大的一定小于等于在最大的里面挑一个最小的。

强对偶条件：$d^*=p^*$，则 strong duality holds. not in general，但是在 SVM 这里是成立的。

斯拉特条件（Slater’s Condition）：当目标函数为凸，且约束为线性，则强对偶条件满足。（证明略）

回忆：

$$\begin{aligned} p^* &= \min_{w,b} \max_{\alpha_i \ge 0} L(w,b, \alpha) \\ d^* &= \max_{\alpha_i\ge 0}\min_{w,b}L(w,b,\alpha) \end{aligned}$$

证明弱对偶条件：假设 $w_p,b_p$ 为 $p^*$ 的解，$\alpha_d$ 为 $d^*$ 的解。则

$$\begin{aligned} p^* = \min_{w,b}\max_{\alpha_i \ge 0}L(w,b,\alpha) &= \max_{\alpha\ge 0} L(w_p,b_p, \alpha) \\ &\ge L(w_p,b_p,\alpha_d)\\ &\ge \min_{w,b}L(w,b,\alpha_d)\\ &= d^* \end{aligned}$$

而我们知道，若强对偶条件成立，则 $p^*$ 与 $d^*$ 的解是一样的，即 $(w_p,b_p, \alpha_d)$，即上面式子中所有的不等号都是等号。这告诉我们，可以通过解对偶问题 $d^*$ 来解原问题。

$$\max_{\alpha\ge 0}\min_{w,b}L(w,b,\alpha) = \frac{1}{2} \left\| w^{2} \right\| + \sum_{i \in [n]} \alpha_i - \sum_{i \in [n]} \alpha_i y_i(w^Tx_i +b)$$

先看里层的。由其凸性，进行求导，要求 $\displaystyle \frac{\partial L}{\partial w} = 0$，$\displaystyle \frac{\partial L}{\partial b} = 0$

$$\begin{aligned} \frac{\partial L}{\partial w} &= w - \sum \alpha_i y_i x_i = 0 \\ \frac{\partial L}{\partial b} &= -\sum \alpha_i y_i = 0 \end{aligned}$$

这不就是 KKT 条件吗，原因就在于由于强对偶性，解是一样的，所以自然也需要满足 KKT 条件。

所以

$$w = \sum_{i \in [n]} \alpha_i y_i x_i \\ \sum_{i \in [n]} \alpha_i y_i = 0$$

将其代入原来的式子，就有

$$\begin{aligned} \max_{\alpha\ge 0}\min_{w,b}L(w,b,\alpha) &= \frac{1}{2} \left\| w^{2} \right\| + \sum_{i \in [n]} \alpha_i - \sum_{i \in [n]} \alpha_i y_i(w^Tx_i +b)\\ &=\max_{\alpha\ge 0} \frac{1}{2} \left( \sum_{i \in [n]} \alpha_i y_i x_i^T \right) \left( \sum_{i \in [n]} \alpha_i y_i x_i\right) + \sum_{i \in [n]} a_i \\ & ~ ~ ~ ~ - \sum_{i \in [n]} \alpha_i y_i \left( \sum_{i \in [n]}\alpha_i y_i x_i^T \right) ^T x_i - b \sum_{i \in [n]} \alpha_i y_i\\ &= \max_{\alpha \ge 0} \sum_{i \in [n]} \alpha_i - \frac{1}{2} \sum_{i \in [n]}\sum_{j \in [n]} \alpha_i \alpha_j y_i y_j x_i^T x_j \end{aligned}$$

subject to $\displaystyle \begin{cases} \alpha_i\ge 0, & \forall i\in [n] \\ \sum a_i y_i = 0, & \forall i \in [n] \end{cases}$，优化问题变为优化 $n$ 个 $\alpha_i$，原来的原始形式则是优化 $d+1$ 个变量。

假设将 $\alpha^*$ 解出来了，考虑解 $w^*,b^*$：

首先显然

$$w^* = \sum_{i\in [n]}\alpha_i y_i x_i$$

然后，对于支持向量 $(x_k,y_k)$，有 $y_k(w^{*T}x_k + b^*)=1$，所以 $b^* = y_k - w^{*T}x_k$，这也告诉我们 $\displaystyle \frac{1}{y_k} = y_k$。

然后对于 active 的约束，$\alpha_i^*>0$。

其实，只需要支持向量就够了。

$$w^* = \sum_{(x_i,y_i)\text{ is a S.V.}}\alpha_i^*y_i x_i$$

SMO 算法（sequential minimum optimization）

刚才我们是假设求解出来了对偶问题，现在考虑如何求解。

1. 主要思路：迭代地更新 $\alpha_i$，而固定其他的 $\alpha_j$。

2. 但是 $\sum \alpha_i y_i = 0$，所以若固定了其他的 $n-1$ 个 $\alpha_j$，$\alpha_i$ 就已经可以被确定了，所以不能简单地这样去做。

   改进：每次挑两个 $\alpha_i$ 和 $\alpha_j$，而固定其他的 $n-2$ 个。注意到 $\displaystyle \alpha_i y_i + \alpha_j y_j= -\sum_{k \ne i,j} \alpha_k y_k = \text{Constant}$。于是可以用 $\alpha_i$ 表示 $\alpha_j$。

3. 解这个一维的二次规划（另外 $n-2$ 个被固定了，选的一个可以表示另一个），这自然是好解的，甚至有闭式解。

4. 重复上述步骤，每次取 $\alpha_i,\alpha_j$，迭代到你想结束为止。

核技巧（Kernel Trick）

考虑对 $x_i$ 做变换 $\varphi(x_i)$（可以是变换到高维空间）

然后便可以将 $\varphi(x_i)^T \varphi(x_j)^T$ 表示为 $k(x_i,x_j)$，这表示了 $x_i$ 与 $x_j$ 的相似度。其实，原来的 $x_i^T x_j$ 也算一种核（线性核）

假设 $x$ 为一维，但线性不可分。而用一个核函数 $\varphi(x) = (x,x^{2})$，其就可以线性可分了：

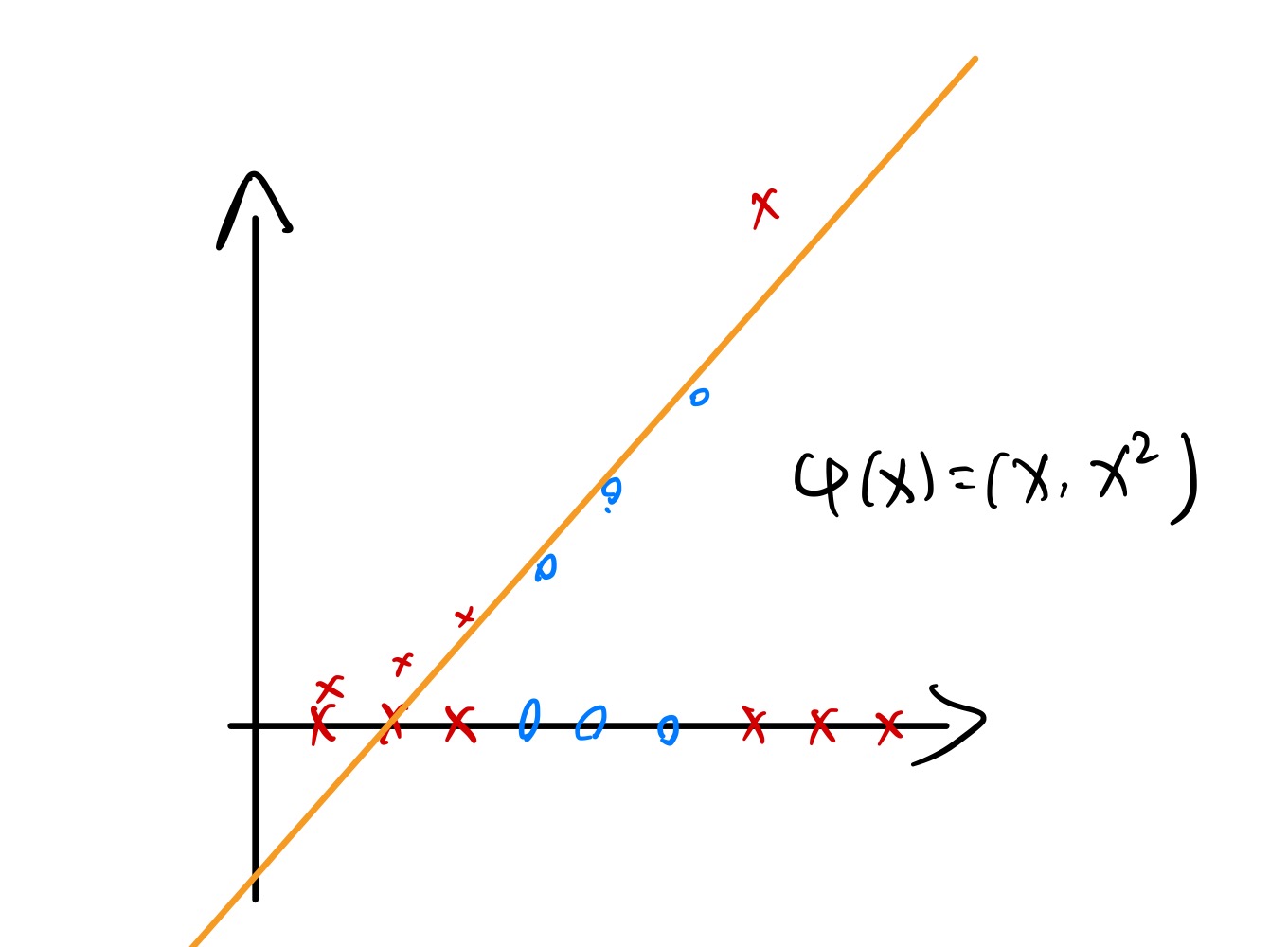
所以这就为我们提供了方便：把本来非线性可分原始数据用核函数进行升维，变为线性可分后用 SVM 求解，求解到的超平面还可以映射回原空间（当然就变得非线性了）

现在，考虑 $x = (x_1,x_2)^T \in \mathbb{R}^2$，定义 $\varphi(x) = (1, x_1, x_2, x_1^{2},x_2^{2},x_1x_2) \in \mathbb{R}^6$，计算的时候有两种方法：

1. 可以直接算所有的 $\varphi(x_i)^T \varphi(x_j) \in \mathbb{R}^6$，相当于先映射到高维空间后做计算，但这样计算的复杂度也会相应高；
2. 在低维空间用 $k(x_i,x_j)$ 直接把他们的相似度算出来（kernel trick），就不需要先把他们映射到高维空间了。

E. g. 考虑 $x = (x_1,x_2)^T,z=(z_1,z_2)^T$，定义核函数 $k(x,z) = (x^Tz+1)^2$。展开：

$$\begin{aligned} k(x,z) &= (x^Tz+1)^{2}\\ &= (x_1 z_1 + x_2 z_2 + 1)^2 \\ &= x_1^{2}z_1^{2}+x_2^{2}z_2^{2}+1+2x_1z_1+2x_2z_2+2x_1z_1x_2z_2\\ &= (1, \sqrt{2}x_1,\sqrt{2}x_2,x_1^{2},x_2^{2},\sqrt{2}x_1x_2)^T \cdot (1,\sqrt{2} z_1, \sqrt{2} z_2, z_1^{2},z_2^{2},\sqrt{2} z_1z_2) \end{aligned}$$

那其实便可看出来 $\varphi(x) = (1, \sqrt{2}x_1,\sqrt{2}x_2,x_1^{2},x_2^{2},\sqrt{2}x_1x_2)^T$，若用了 kernel trick 显然就能达到更低的时间复杂度。

核函数合法性的判断：$k(\cdot ,\cdot )$ 合法仅当 $\exists \varphi$ 使得 $k(x,z) = \varphi(x)^T \varphi(z)^T$。显然一个输出负数的核函数绝对是不合法的。接下来介绍 Mercer Theorem：$k(\cdot ,\cdot )$ 合法当且仅当：

1. 对称性：$k(x,z) = k(z,x), \forall x,z$
2. 核矩阵（kernel matrix, gram matrix）半正定

   $$K := \begin{bmatrix} k(x_1,x_1) & k(x_1,x_2) & \cdots & k(x_1,x_n) \\ \vdots & \vdots & & \vdots \\ k(x_n,x_1) & k(x_n,x_2) & \cdots & k(x_n,x_n) \\\end{bmatrix}\in \mathbb{R}^{n\times n}$$

这里不打算证明，给出一个 intuition：$K$ 对称且半正定所以肯定可以对角化，且所有特征值 $\ge 0$。则 $K= \sum_k \lambda_k \mu_k \mu_k^T$，$K_{ij} = \sum_k \lambda_k \mu_{kj} \mu_{ki}$，所以这样其实已经将 $\varphi$ 给出。（不考）

常见的核函数：

• 线性核：$k(x,z) = x^T z$；
• 多项式核：$k(x,z) = (x^Tz + 1)^p$，$\mathbb{R}^d \to \mathbb{R}^{O(\min(p^d,d^p))}$；
• 高斯核（RBF Kernel，radial basis function）：

  $$k(x,z) = \exp\left( - \frac{\left\| x-z \right\|^{2}}{2\sigma^2} \right)$$

高斯核相当于把 $x$ 映射到无穷维空间然后做内积？考虑泰勒展开：

$$f(x) = f(0)+f'(0)x+\frac{f''(0)}{2!}x^{2}+ \cdots$$

将 $k(x,z)$ 写出来：

$$\begin{aligned} k(x,z)&= \exp\left( -\frac{\left\| x \right\|^2}{2\sigma^{2}} \right) \exp\left( -\frac{\left\| z \right\|^2}{2\sigma^{2}} \right) \exp\left(\frac{1}{\sigma^{2}}x^Tz\right) \\ \end{aligned}$$

将最后一项进行泰勒展开：

$$\begin{aligned} &\exp\left(\frac{1}{\sigma^{2}}x^Tz\right) \\ =& 1+ \frac{1}{\sigma^{2}} x^Tz + \frac{1}{2!} \frac{(x^Tz)^{2}}{(\sigma^{2})^{2}} + \frac{1}{3!}\frac{(x^Tz)^3}{(\sigma^{2})^3}+ \cdots \end{aligned}$$

后面是一堆多项式核的叠加！根据前面的定理，合法的核函数相加后仍然合法。

事实上，$\sigma$ 是很重要的超参数。更大的 $\sigma^{2}$ 会使得高阶项迅速趋于 $0$，有效的维度就会降低；小的 $\sigma^{2}$ 有可能让任意的数据均可分，带来过拟合的风险，对 outlier 不健壮。

松弛变量（slack variables）

现在问题的关键在于如何处理离群点（outliers）。

之前，我们都是硬约束，即要求 $\forall i, y_i(w^Tx_i+b)\ge 1$。现在考虑软约束，引入松弛变量（slack variables）$\xi_i$。

现在约束变成 $\forall i \in [n], y_i(w^T x_i +b)\ge 1-\xi_i$，其中 $\xi_i\ge 0$（允许超过 $w^Tx+b=\pm 1$ 一定距离 $\xi_i$）

但同时，肯定不能让 $\xi_i$ 任意优化。我们肯定希望 $\xi_i$ 尽可能小。优化问题变成：

$$\min_{w,b,\xi} \frac{1}{2} \left\| w \right\|^{2} + C \cdot \sum_{i \in [n]} \xi_i$$

s. t. $y_i(w^Tx_i) \ge 1 - \xi_i, \xi_i\ge 0,\forall i \in [n]$。其中 $C$ 为调控 $\xi$ 力度的参数。事实上这才是 SVM 实战中最常用的形式。

注意到 $\xi_i\ge \max(0, 1-y_i(w^T x_i+b))$，所以问题可以进一步化简：

$$\min_{w,b} \frac{1}{2} \left\| w \right\|^{2}+C\cdot \sum_{i \in [n]}\max(0, 1-y_i(w^T x_i+b))$$

这里是直接用 $\xi$ 的下界去进行替换。而且注意到 $\max(0, 1-y_i(w^Tx_i+b))$ 其实为合页损失（hinge loss）。定义 $z_i:= y_i f(x_i)$

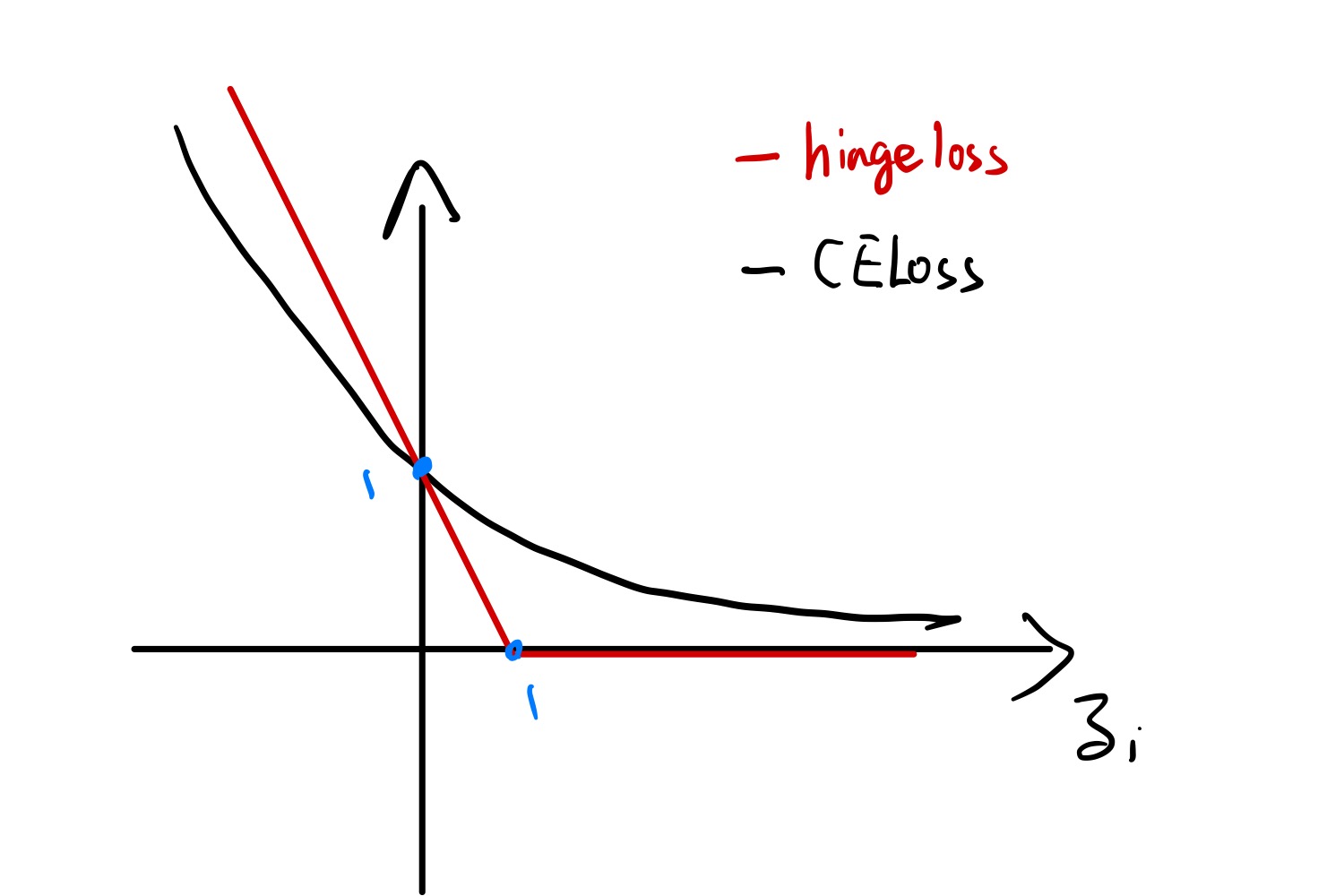
$z_i>1$ 的情况相当于点不产生贡献，$z_i <1$ 的情况就对应着 $\xi_i>0$ 的情况，产生正比于 $\xi_i$ 的 loss。而这个时候 $\left\| w \right\|^2$ 就可以理解为正则化项了（倒反天罡）。