24秋机器学习笔记-lec5

SVM 对偶形式 (cont.)

回忆：

$$\begin{aligned} p^* &= \min_{w,b} \max_{\alpha_i \ge 0} L(w,b, \alpha) \\ d^* &= \max_{\alpha_i\ge 0}\min_{w,b}L(w,b,\alpha) \end{aligned}$$

证明弱对偶条件：假设 $w_p,b_p$ 为 $p^*$ 的解，$\alpha_d$ 为 $d^*$ 的解。则

$$\begin{aligned} p^* = \min_{w,b}\max_{\alpha_i \ge 0}L(w,b,\alpha) &= \max_{\alpha\ge 0} L(w_p,b_p, \alpha) \\ &\ge L(w_p,b_p,\alpha_d)\\ &\ge \min_{w,b}L(w,b,\alpha_d)\\ &= d^* \end{aligned}$$

而我们知道，若强对偶条件成立，则 $p^*$ 与 $d^*$ 的解是一样的，即 $(w_p,b_p, \alpha_d)$，即上面式子中所有的不等号都是等号。这告诉我们，可以通过解对偶问题 $d^*$ 来解原问题。

$$\max_{\alpha\ge 0}\min_{w,b}L(w,b,\alpha) = \frac{1}{2} \left\| w^{2} \right\| + \sum_{i \in [n]} \alpha_i - \sum_{i \in [n]} \alpha_i y_i(w^Tx_i +b)$$

先看里层的。由其凸性，进行求导，要求 $\displaystyle \frac{\partial L}{\partial w} = 0$，$\displaystyle \frac{\partial L}{\partial b} = 0$

$$\begin{aligned} \frac{\partial L}{\partial w} &= w - \sum \alpha_i y_i x_i = 0 \\ \frac{\partial L}{\partial b} &= -\sum \alpha_i y_i = 0 \end{aligned}$$

这不就是 KKT 条件吗，原因就在于由于强对偶性，解是一样的，所以自然也需要满足 KKT 条件。

所以

$$w = \sum_{i \in [n]} \alpha_i y_i x_i \\ \sum_{i \in [n]} \alpha_i y_i = 0$$

将其代入原来的式子，就有

$$\begin{aligned} \max_{\alpha\ge 0}\min_{w,b}L(w,b,\alpha) &= \frac{1}{2} \left\| w^{2} \right\| + \sum_{i \in [n]} \alpha_i - \sum_{i \in [n]} \alpha_i y_i(w^Tx_i +b)\\ &=\max_{\alpha\ge 0} \frac{1}{2} \left( \sum_{i \in [n]} \alpha_i y_i x_i^T \right) \left( \sum_{i \in [n]} \alpha_i y_i x_i\right) + \sum_{i \in [n]} a_i \\ & ~ ~ ~ ~ - \sum_{i \in [n]} \alpha_i y_i \left( \sum_{i \in [n]}\alpha_i y_i x_i^T \right) ^T x_i - b \sum_{i \in [n]} \alpha_i y_i\\ &= \max_{\alpha \ge 0} \sum_{i \in [n]} \alpha_i - \frac{1}{2} \sum_{i \in [n]}\sum_{j \in [n]} \alpha_i \alpha_j y_i y_j x_i^T x_j \end{aligned}$$

subject to $\displaystyle \begin{cases} \alpha_i\ge 0, & \forall i\in [n] \\ \sum a_i y_i = 0, & \forall i \in [n] \end{cases}$，优化问题变为优化 $n$ 个 $\alpha_i$，原来的原始形式则是优化 $d+1$ 个变量。

假设将 $\alpha^*$ 解出来了，考虑解 $w^*,b^*$：

首先显然

$$w^* = \sum_{i\in [n]}\alpha_i y_i x_i$$

然后，对于支持向量 $(x_k,y_k)$，有 $y_k(w^{*T}x_k + b^*)=1$，所以 $b^* = y_k - w^{*T}x_k$，这也告诉我们 $\displaystyle \frac{1}{y_k} = y_k$。

然后对于 active 的约束，$\alpha_i^*>0$。

其实，只需要支持向量就够了。

$$w^* = \sum_{(x_i,y_i)\text{ is a S.V.}}\alpha_i^*y_i x_i$$

SMO 算法（sequential minimum optimization）

刚才我们是假设求解出来了对偶问题，现在考虑如何求解。

1. 主要思路：迭代地更新 $\alpha_i$，而固定其他的 $\alpha_j$。

2. 但是 $\sum \alpha_i y_i = 0$，所以若固定了其他的 $n-1$ 个 $\alpha_j$，$\alpha_i$ 就已经可以被确定了，所以不能简单地这样去做。

   改进：每次挑两个 $\alpha_i$ 和 $\alpha_j$，而固定其他的 $n-2$ 个。注意到 $\displaystyle \alpha_i y_i + \alpha_j y_j= -\sum_{k \ne i,j} \alpha_k y_k = \text{Constant}$。于是可以用 $\alpha_i$ 表示 $\alpha_j$。

3. 解这个一维的二次规划（另外 $n-2$ 个被固定了，选的一个可以表示另一个），这自然是好解的，甚至有闭式解。

4. 重复上述步骤，每次取 $\alpha_i,\alpha_j$，迭代到你想结束为止。

核技巧（Kernel Trick）

考虑对 $x_i$ 做变换 $\varphi(x_i)$（可以是变换到高维空间）

然后便可以将 $\varphi(x_i)^T \varphi(x_j)^T$ 表示为 $k(x_i,x_j)$，这表示了 $x_i$ 与 $x_j$ 的相似度。其实，原来的 $x_i^T x_j$ 也算一种核（线性核）

假设 $x$ 为一维，但线性不可分。而用一个核函数 $\varphi(x) = (x,x^{2})$，其就可以线性可分了：

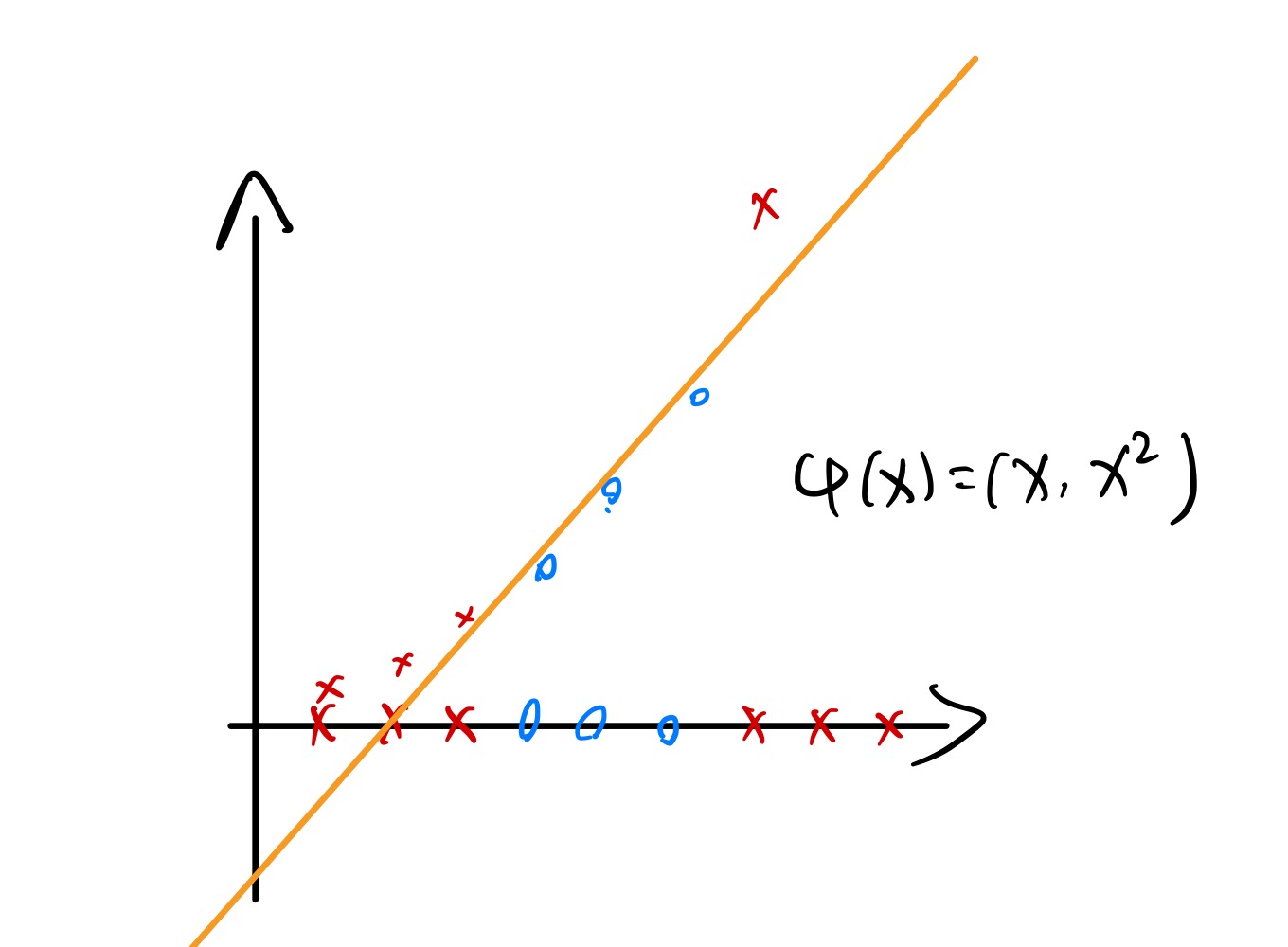
所以这就为我们提供了方便：把本来非线性可分原始数据用核函数进行升维，变为线性可分后用 SVM 求解，求解到的超平面还可以映射回原空间（当然就变得非线性了）

现在，考虑 $x = (x_1,x_2)^T \in \mathbb{R}^2$，定义 $\varphi(x) = (1, x_1, x_2, x_1^{2},x_2^{2},x_1x_2) \in \mathbb{R}^6$，计算的时候有两种方法：

1. 可以直接算所有的 $\varphi(x_i)^T \varphi(x_j) \in \mathbb{R}^6$，相当于先映射到高维空间后做计算，但这样计算的复杂度也会相应高；
2. 在低维空间用 $k(x_i,x_j)$ 直接把他们的相似度算出来（kernel trick），就不需要先把他们映射到高维空间了。

E. g. 考虑 $x = (x_1,x_2)^T,z=(z_1,z_2)^T$，定义核函数 $k(x,z) = (x^Tz+1)^2$。展开：

$$\begin{aligned} k(x,z) &= (x^Tz+1)^{2}\\ &= (x_1 z_1 + x_2 z_2 + 1)^2 \\ &= x_1^{2}z_1^{2}+x_2^{2}z_2^{2}+1+2x_1z_1+2x_2z_2+2x_1z_1x_2z_2\\ &= (1, \sqrt{2}x_1,\sqrt{2}x_2,x_1^{2},x_2^{2},\sqrt{2}x_1x_2)^T \cdot (1,\sqrt{2} z_1, \sqrt{2} z_2, z_1^{2},z_2^{2},\sqrt{2} z_1z_2) \end{aligned}$$

那其实便可看出来 $\varphi(x) = (1, \sqrt{2}x_1,\sqrt{2}x_2,x_1^{2},x_2^{2},\sqrt{2}x_1x_2)^T$，若用了 kernel trick 显然就能达到更低的时间复杂度。

核函数合法性的判断：$k(\cdot ,\cdot )$ 合法仅当 $\exists \varphi$ 使得 $k(x,z) = \varphi(x)^T \varphi(z)^T$。显然一个输出负数的核函数绝对是不合法的。接下来介绍 Mercer Theorem：$k(\cdot ,\cdot )$ 合法当且仅当：

1. 对称性：$k(x,z) = k(z,x), \forall x,z$
2. 核矩阵（kernel matrix, gram matrix）半正定

   $$K := \begin{bmatrix} k(x_1,x_1) & k(x_1,x_2) & \cdots & k(x_1,x_n) \\ \vdots & \vdots & & \vdots \\ k(x_n,x_1) & k(x_n,x_2) & \cdots & k(x_n,x_n) \\\end{bmatrix}\in \mathbb{R}^{n\times n}$$

这里不打算证明，给出一个 intuition：$K$ 对称且半正定所以肯定可以对角化，且所有特征值 $\ge 0$。则 $K= \sum_k \lambda_k \mu_k \mu_k^T$，$K_{ij} = \sum_k \lambda_k \mu_{kj} \mu_{ki}$，所以这样其实已经将 $\varphi$ 给出。（不考）

常见的核函数：

• 线性核：$k(x,z) = x^T z$；
• 多项式核：$k(x,z) = (x^Tz + 1)^p$，$\mathbb{R}^d \to \mathbb{R}^{O(\min(p^d,d^p))}$；
• 高斯核（RBF Kernel，radial basis function）：

  $$k(x,z) = \exp\left( - \frac{\left\| x-z \right\|^{2}}{2\sigma^2} \right)$$

高斯核相当于把 $x$ 映射到无穷维空间然后做内积？考虑泰勒展开：

$$f(x) = f(0)+f'(0)x+\frac{f''(0)}{2!}x^{2}+ \cdots$$

将 $k(x,z)$ 写出来：

$$\begin{aligned} k(x,z)&= \exp\left( -\frac{\left\| x \right\|^2}{2\sigma^{2}} \right) \exp\left( -\frac{\left\| z \right\|^2}{2\sigma^{2}} \right) \exp\left(\frac{1}{\sigma^{2}}x^Tz\right) \\ \end{aligned}$$

将最后一项进行泰勒展开：

$$\begin{aligned} &\exp\left(\frac{1}{\sigma^{2}}x^Tz\right) \\ =& 1+ \frac{1}{\sigma^{2}} x^Tz + \frac{1}{2!} \frac{(x^Tz)^{2}}{(\sigma^{2})^{2}} + \frac{1}{3!}\frac{(x^Tz)^3}{(\sigma^{2})^3}+ \cdots \end{aligned}$$

后面是一堆多项式核的叠加！根据前面的定理，合法的核函数相加后仍然合法。

事实上，$\sigma$ 是很重要的超参数。更大的 $\sigma^{2}$ 会使得高阶项迅速趋于 $0$，有效的维度就会降低；小的 $\sigma^{2}$ 有可能让任意的数据均可分，带来过拟合的风险，对 outlier 不健壮。

松弛变量（slack variables）

现在问题的关键在于如何处理离群点（outliers）。

之前，我们都是硬约束，即要求 $\forall i, y_i(w^Tx_i+b)\ge 1$。现在考虑软约束，引入松弛变量（slack variables）$\xi_i$。

现在约束变成 $\forall i \in [n], y_i(w^T x_i +b)\ge 1-\xi_i$，其中 $\xi_i\ge 0$（允许超过 $w^Tx+b=\pm 1$ 一定距离 $\xi_i$）

但同时，肯定不能让 $\xi_i$ 任意优化。我们肯定希望 $\xi_i$ 尽可能小。优化问题变成：

$$\min_{w,b,\xi} \frac{1}{2} \left\| w \right\|^{2} + C \cdot \sum_{i \in [n]} \xi_i$$

s. t. $y_i(w^Tx_i) \ge 1 - \xi_i, \xi_i\ge 0,\forall i \in [n]$。其中 $C$ 为调控 $\xi$ 力度的参数。事实上这才是 SVM 实战中最常用的形式。

注意到 $\xi_i\ge \max(0, 1-y_i(w^T x_i+b))$，所以问题可以进一步化简：

$$\min_{w,b} \frac{1}{2} \left\| w \right\|^{2}+C\cdot \sum_{i \in [n]}\max(0, 1-y_i(w^T x_i+b))$$

这里是直接用 $\xi$ 的下界去进行替换。而且注意到 $\max(0, 1-y_i(w^Tx_i+b))$ 其实为合页损失（hinge loss）。定义 $z_i:= y_i f(x_i)$

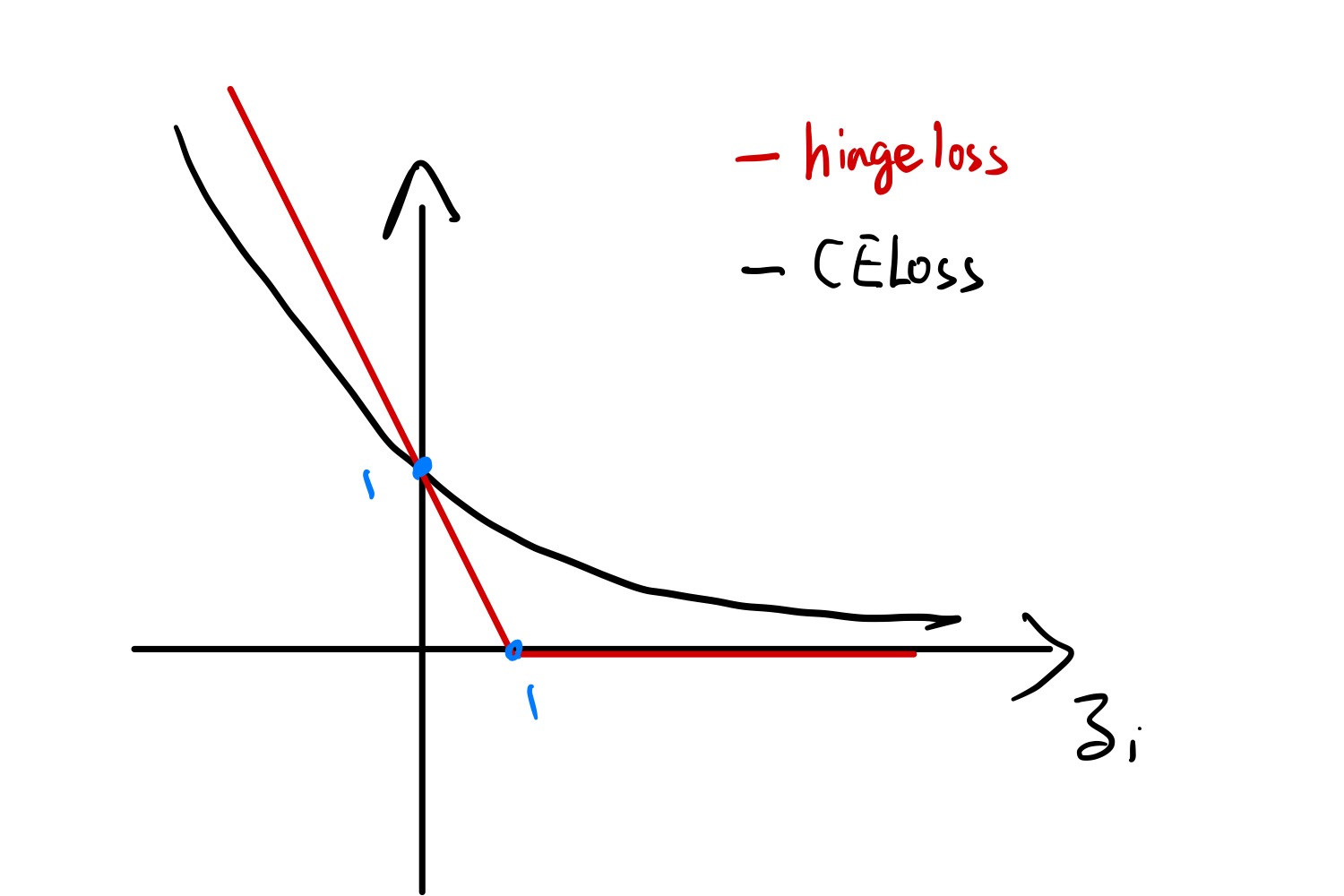
$z_i>1$ 的情况相当于点不产生贡献，$z_i <1$ 的情况就对应着 $\xi_i>0$ 的情况，产生正比于 $\xi_i$ 的 loss。而这个时候 $\left\| w \right\|^2$ 就可以理解为正则化项了（倒反天罡）。