24秋机器学习笔记-11-生成式模型

本文主要涉及无监督学习中的生成式模型，介绍了 VAE 与 DDPM。

在阅读本篇之前建议先阅读10-无监督学习。

张老师关于 VAE 的推导和讲解非常精彩，强烈建议动手跟着推一遍。

一键回城。

VAE（变分自编码器，Variational Autoencoder）

引入

在上篇笔记中的 MoG 其实已经是种生成式模型了，但其只能用于处理成簇/低维的数据（会面临维度灾难：高维下数据点之间的欧氏距离没有那么好的实际意义了）

一种高维数据的代表是图片。比如我们知道 $x \sim p(x)$，但是一般而言从 $p(x)$ 中采样是比较困难的。但是像均匀分布 $U([a,b])$ 和高斯分布这样比较简单的分布还是比较容易采样的。

一种思路是，从一个简单的分布（如 $[0,1]$ 高斯分布）中采样一个隐变量 $z$，然后用一个函数（可以是一个神经网络）$f(z;\theta)$ 将 $z$ 映射到 $x$（可以是图片）。事实上这也是市面上大多数生成式模型的基本思路。

此时 $p(x)$ 可以写成

$$p(x) = \int_z p(x\mid z; \theta) \cdot p(z)\mathrm{d}z$$

为添加随机噪声可以用 $\mathcal{N}(x\mid f(z;\theta), \sigma^2I)$ 来代替 $p(x\mid z; \theta)$，$p(z)$ 可以就是简单的 $p(z) = \mathcal{N}(z\mid 0, I)$。和 MoG 不一样的是，此时 $z$ 是连续的，所以要写成积分。

所以就使用 MLE 来优化 $\theta$，最大化 $\displaystyle \max_{\theta} \sum_{i \in [n]} \log p(x_i)$。那么如何优化之呢？

• SGD？一个很大的问题在于，我们需要计算 $z$ 在其全空间上的积分，而这是无法直接计算的，如果用蒙特卡洛方法来近似的话，需要进行巨量采样以较为准确地近似，而且 $z$ 的维度过高，故也是不行的。且考虑到 $x_i$ 的数量 $n$ 在实际中也是非常大的，所以不能使用 SGD。
• EM？优化这种带隐变量的 $p(x)$ 确实能让人想起 EM。在 E-step 中要计算后验 $p(z_i\mid x_i;\theta^{\text{old}})$，在 M-step 中要最大化 $\displaystyle \max_{\theta} \int_z p(z_i\mid x_i; \theta^{\text{old}})p(x_i,z_i;\theta)\mathrm{d}z$。但是在 E-step 这一步，回想 MoG 中，要计算的是 $\displaystyle \frac{p(x_i\mid z_i)\cdot p(z_i)}{\sum_{z_i}p(x_i\mid z_i)\cdot p(z_i)}$，$z_i$ 的取值是有限的（$k$ 种），但是在当前的问题里面其变为 $\displaystyle \frac{p(x_i\mid z_i)\cdot p(z_i)}{\int_{z_i}p(x_i\mid z_i)\cdot p(z_i)}$，这个积分也是没法算的。

SGD 和 EM 都不 work 了，核心问题在于隐变量的后验 $p(z\mid x;\theta)$ 不好计算。

ELBO 推导

解决方案：引入一个变分分布（variational distribution）$q(z\mid x;\theta')$ 来近似 $p(z\mid x;\theta)$。注意这个变分分布是有自己的参数 $\theta'$ 的，在 EM 中因为推出来其就是上一步的旧参数所以就没有单独写出来自己的参数。

接下来就是推导 ELBO 了，根据上一篇笔记的内容，我们知道

$$\log p(x;\theta) = \sum_z q(z\mid x)\cdot \log \frac{p(x,z;\theta)}{q(z\mid x)} - \sum_z q(z\mid x) \cdot \log \frac{p(z\mid x;\theta)}{q(z\mid x)}$$

等号右边第一项就是 ELBO，第二项就是 $q(z\mid x)$ 和 $p(z\mid x;\theta)$ 的 KL 散度。

不过 ELBO 事实上可以直接认为是 $\mathrm{ELBO} = \log p(x) - \mathrm{KL}(q\parallel p)$。推导：

$$\begin{aligned} \mathrm{ELBO} &= \log p(x;\theta) - \mathrm{KL}(q(z\mid x;\theta')\parallel p(z\mid x;\theta)) \\ &= \log p(x;\theta) - \int_z q(z\mid x;\theta')\cdot \log \frac{q(z\mid x;\theta')}{p(z\mid x;\theta)}\mathrm{d}z\\ &= \int_z q(z\mid x;\theta') \log p(x;\theta) \mathrm{d}z - \int_z q(z\mid x;\theta')\cdot \log \frac{q(z\mid x;\theta')}{p(z\mid x;\theta)}\mathrm{d}z\\ &= \int_z q(z\mid x;\theta') \log \frac{p(x;\theta) p(z\mid x;\theta)}{q(z\mid x;\theta')}\mathrm{d}z\\ &= \int_z q(z\mid x;\theta') \log \frac{p(x,z;\theta)}{q(z\mid x;\theta')} \end{aligned}$$

发现和上一篇笔记里面得到的 ELBO 是一样的。实际中推导 ELBO 一般就使用这种方法，比较简单。注意第三行里面 $\displaystyle \int_z q(z\mid x;\theta') \mathrm{d}z = 1$，凑这个项是为了和减号右边的东西更好配凑。

ELBO 和实际的对数似然之间相差的就是那个 KL 散度，所以用 ELBO 的效果好不好就取决于 $q$ 是否足够接近 $p(z\mid x;\theta)$。

这个 ELBO 怎么优化？

其实还是通过采样 $z$ 来近似计算这个积分，然后用梯度下降。在前面我们说过梯度下降不 work，但为什么在这里就 work 了呢？

在前面的情况，我们为了采样 $z$ 需要在 $z$ 的先验分布（通常是个高维高斯分布）里面“漫无目的”地进行采样，高维潜在空间中的绝大多数 $z$ 对 $p(x\mid z)$ 的贡献几乎为零，导致蒙特卡洛估计需要极多样本才能降低方差，计算代价过高，且梯度估计的方差会很高。

但是在 ELBO 中，$z$ 是在变分分布（近似后验） $q(z\mid x;\theta')$ 中采样的样本集中在 $p(x\mid z)$ 中有显著贡献的区域，极大提升了采样效率。

• 在 EM 中，我们是交替地优化 $\theta$ 和 $q$（固定一个优化另一个）；
• 在 VAE 中，我们是同时优化 $\theta$ 和 $q(\theta')$。

关于对 ELBO 的另一种直接推导：

$$\begin{aligned} \log p(x) &= \log \int_z p(x\mid z)q(z) \mathrm{d}z\\ &= \log \mathbb{E}_{z \sim q(z)} \left[ \log \frac{p(x,z)}{q(z)} \right]\\ &\ge \mathbb{E}_{z \sim q(z)} \left[ \log \frac{p(x,z)}{q(z)} \right] & \text{Jensen Inequality} \end{aligned}$$

最后得到的那个东西事实上就是 ELBO。

AE 简介

在继续推导 VAE 的具体形式之前，我们先来看一下何为 AE（autoencoder）。

如上图所示，一个 AE 由两个神经网络组成，分别称为编码器 encoder 和解码器 decoder。编码器负责将原始数据 $x$ 压缩到一个更小的空间中，即生成隐变量 $z$。解码器则负责根据隐变量 $z$ 还原出 $\tilde x$。朴素 AE 的 loss 就看 decoder 重建出来的效果。

一个想法是：随机采样 $z$，然后直接让其过 decoder，这样其就是一个生成式模型了。但是朴素的 AE 一般不太 work，因为 encoder 生成的 $z$ 的分布是不太好采样的，其可能散落在高维空间的各个角落，所以随机采样的 $z$ 生成出来的 $\tilde x$ 大概率是不太有道理的。

而 VAE 的想法就是将 $z$ 集中在各向同性的标准高斯分布 $\mathcal{N}(0,I)$ 附近（由下式的 KL 散度实现），VAE 最终形式的损失函数为

$$\min \{\text{reconstruction loss} + \mathrm{KL}(q(z\mid x;\theta')\parallel p(z) \sim \mathcal{N}(0,I)) \}$$

那么我们要生成图片的时候从 $\mathcal{N}(0,I)$ 中采样 $z$，就能生成比较有道理的图片了。那么怎么推导呢？

VAE 损失函数推导

首先重写一下 ELBO：

$$\begin{aligned} \mathrm{ELBO} &= \int_z q(z\mid x;\theta') \log \frac{p(x,z;\theta)}{q(z\mid x;\theta')} \\ &= \int_z q(z\mid x;\theta') \log p(x\mid z;\theta) \mathrm{d}z + \int_z q(z\mid x;\theta') \log \frac{p(z)}{q(z\mid x;\theta')}\mathrm{d}z\\ &= \int_z q(z\mid x;\theta') \log p(x\mid z;\theta) \mathrm{d}z - \mathrm{KL}(q(z\mid x;\theta')\parallel p(z)) \end{aligned}$$

$\displaystyle \mathrm{KL}(q(z\mid x;\theta')\parallel p(z))$ 就是 encoder 与 $z$ 的先验之间的 divergence（最大化 ELBO，所以要最小化这个 KL）。

$\displaystyle \int_z q(z\mid x;\theta') \log p(x\mid z;\theta) \mathrm{d}z$ 可以看成 reconstruction quality。实际中建模成 $p(x\mid z;\theta) = \mathcal{N}(x\mid f(z,\theta), \sigma^{2}I)$。所以

$$\begin{aligned} \log p(x\mid z;\theta) &= \log \frac{1}{(2\pi \sigma)^{\frac{d}{2}}}\exp\left( -\frac{\left\| f(z;\theta) - x \right\|^{2}}{2\sigma^{2}} \right) \\ &= C - \frac{1}{2\sigma^{2}}\left\| f(z;\theta) - x \right\|^{2} \end{aligned}$$

为了最大化 $\displaystyle \int_z q(z\mid x;\theta') \log p(x\mid z;\theta) \mathrm{d}z$，就要最小化 $\left\| f(z;\theta) - x \right\|^{2}$，我们管这个东西就叫做重建误差 reconstruction loss。

按理来说我们为了算一个 $x$ 的 recon loss 是需要从 $q(z\mid x;\theta')$ 中采样很多个 $z$ 来算这个积分的，但是实际操作中对每个 $x_i$ 只采样一个 $z_i$。这样类似 SGD，可以提升随机性，缓解过拟合。

到这个时候我们就可以看一下 VAE 的大概结构了。我们将编码器 $q(z\mid x; \theta')$ 也看成高斯分布 $\mathcal{N}(z\mid \mu(x;\theta'), \Sigma(x;\theta'))$，只不过 $\mu$ 由神经网络给出，$\Sigma$ 一般为对角阵（也由神经网络计算）。对于前向传播，输入一个 $x$，然后从这个分布 $\mathcal{N}(z\mid \mu(x;\theta'), \Sigma(x;\theta'))$ 里面采样一个 $z$，最后生成一个 $\tilde x = f(z;\theta)$（注意这里直接取了 $p(x\mid z)$ 的均值）。对于一个数据集 $\{x_1, \cdots ,x_n\}$，损失函数就可以写为

$$\frac{1}{n}\sum_{i \in [n]}\left[ \left\| \tilde{x_i} - x_i \right\|^{2} + \beta\cdot \mathrm{KL}(q(z\mid x;\theta')\parallel p(z)) \right]$$

$\displaystyle \frac{1}{n}\sum_{i \in [n]}\left\| \tilde{x_i} - x_i \right\|^{2}$ 为 recon loss，前面的常数什么的就直接以 $\beta$ 的形式给到 KL 散度上了。同时由于这是两个高斯分布的 KL 散度，是有闭式解的，所以也很好计算。VAE 的损失函数就这样推导出来了，非常简洁明了。

其中 $\beta$ 为很重要的超参数，如果 $\beta$ 过小，KL 散度不能产生贡献，其就会退化成普通 AE；如果 $\beta$ 过大，recon loss 产生贡献不足，就可能导致在训练数据上都达不到好的重建效果。在实际中，调 $\beta$ 是很重要的一环。

重参数化技巧（Reparameterization Trick）

不过还没完，有一个很重要的问题是，我们在做梯度回传的时候，由于有一个从 $q(z\mid x;\theta')$ 中 采样 $z$ 的操作的存在，我们的梯度在此中断了，没法往回传到 $q(\theta')$ 中。

解决的方法也很简单，我们不从 $\mathcal{N}(z\mid \mu(x;\theta'), \Sigma(x;\theta'))$ 里面直接采样 $z$，而是从标准正态分布 $\mathcal{N}(0,I)$ 中采样一个 $\varepsilon$，然后令 $z = \Sigma(x)^{\frac{1}{2}} \cdot \varepsilon + \mu(x)$。

为什么这样是可行的？

我们接下来证明 $z = \Sigma(x)^{\frac{1}{2}}\cdot \varepsilon+\mu(x) \sim \mathcal{N}(\mu(x),\Sigma(x))$。

均值是显然的，$\mathbb{E}[z] = \mu(x)$。

至于协方差：

$$\begin{aligned} \operatorname{Cov}(z) &= \mathbb{E}[(z - \mathbb{E}[z])(z - \mathbb{E}[z])^T] \\ &= \mathbb{E}[\Sigma(x)^{\frac{1}{2}}\varepsilon \varepsilon^T \Sigma^T(x)^{\frac{1}{2}}]\\ &= \Sigma(x)^{\frac{1}{2}} \mathbb{E}[\varepsilon\varepsilon^T]\Sigma(x)^{\frac{1}{2}}\\ &= \Sigma(x) \end{aligned}$$

第三行到第四行是基于 $\varepsilon \varepsilon^T = I$。

经过重参数化，梯度就可以往前流了，如下图所示：

重参数化技巧的应用：

对于均匀分布的情况 $z \sim U([a,b])$ 也是可以用重参数化技巧的：从 $U([0,1])$ 采样 $\varepsilon$，然后令 $z = \varepsilon(b - a) + a$。

KL 散度的计算

最后一个问题就是如何算 $p(z) = \mathcal{N}(z\mid 0,I)$ 和 $q(z\mid x;\theta') = \mathcal{N}(z\mid \mu(x),\Sigma(x))$ 之间的 KL 散度。

开推：

$$\begin{aligned} \mathrm{KL}(q(z\mid x; \theta')\parallel p(z)) &= \int_z \mathcal{N}(z\mid \mu(x),\Sigma(x)) \log \frac{\mathcal{N}(z\mid \mu(x),\Sigma(x))}{\mathcal{N}(z\mid 0,I)} \\ &= \mathbb{E}_{z \sim \mathcal{N}(z\mid \mu(x),\Sigma(x))}\left[ \log \frac{\frac{1}{(2\pi)^{\frac{d}{2}}}\frac{1}{|\Sigma(x)|^{\frac{1}{2}}}\exp\left( -\frac{1}{2}(z - \mu(x))^T \Sigma(x)^{-1}(z - \mu(x)) \right) }{\frac{1}{(2\pi)^{\frac{d}{2}}}\exp\left( -\frac{1}{2}z^Tz \right) } \right] \\ &= \mathbb{E}_{z \sim \mathcal{N}(z\mid \mu(x),\Sigma(x))}\left[-\frac{1}{2}\log\det\Sigma(x) - \frac{1}{2}(z - \mu(x))^T \Sigma(x)^{-1}(z - \mu(x)) + \frac{1}{2}z^Tz \right] \end{aligned}$$

考虑每一项怎么求。第一项与 $z$ 无关，所以不用管。对于第二项，需要用到一个叫做 trace trick 的方法。因为 $(z - \mu)^T\Sigma^{-1}(z - \mu)$ 是一个标量，所以其与 $\displaystyle \operatorname{tr}\left( (z - \mu)^T\Sigma^{-1}(z - \mu) \right)$ 是相等的。然后基于 $\operatorname{tr}(ABC) = \operatorname{tr}(BCA)=\operatorname{tr}(CAB)$，就可得到

$$\begin{aligned} &\mathbb{E}_z\left[ \operatorname{tr}\left( (z - \mu)^T\Sigma^{-1}(z - \mu) \right) \right] \\ =& \mathbb{E}_z\left[\operatorname{tr}\left( (z - \mu)(z-\mu)^T \Sigma^{-1} \right) \right]\\ =& \operatorname{tr}\left( \mathbb{E}_z\left[{\color{red}{(z-\mu)(z-\mu)^T}}\right] \Sigma^{-1} \right)\\ =& \operatorname{tr}(\Sigma \Sigma^{-1}) = \operatorname{tr}(I) = d \end{aligned}$$

其中 $d$ 为 $z$ 的维度。

最后还有 $\mathbb{E}_z\left[ z^Tz \right]$。我们发现凑出 $\Sigma$ 是一个非常好的事情，所以这里进行一个减 $\mu$ 加 $\mu$ 的方法来配凑出 $\Sigma$：

$$\begin{aligned} \mathbb{E}_z\left[ z^Tz \right] &= \mathbb{E}_z\left[ (z - \mu + \mu)^T(z - \mu + \mu) \right] \\ &= \mathbb{E}_z\left[ (z - \mu)^T(z - \mu) \right] + 2\mathbb{E}_z\left[ (z - \mu)^T \right]\cdot \mu + \mu^T\mu\\ &= \operatorname{tr}(\Sigma) + \mu^T\mu \end{aligned}$$

第二行中的 $\mathbb{E}_z\left[ (z - \mu)^T \right]$ 显然为 $0$，第二行到第三行同样用了 trace trick 来凑出 $\Sigma$。

所以我们最后得到

$$\mathrm{KL}(q(z\mid x; \theta')\parallel p(z)) = -\frac{1}{2}\log\det\Sigma - \frac{1}{2}d + \frac{1}{2}\operatorname{tr}(\Sigma) + \frac{1}{2}\mu^T\mu$$

一般为了简便直接令 $\Sigma$ 为对角阵，$\Sigma(x) = \sigma(x)^2I$，其中 $\sigma(x)^2 \in \mathbb{R}^d$，代表每一维的方差，同样由神经网络给出，则 KL 散度的形式可以写为

$$\mathrm{KL}(q(z\mid x; \theta')\parallel p(z)) = -\frac{1}{2} \sum_{j \in [d]} \log \sigma(x)^2_j - \frac{1}{2}d + \frac{1}{2}\sum_{j \in [d]}\sigma(x)^2_j + \frac{1}{2}\mu^T(x)\mu(x)$$

实际中神经网络输出的为 $\log \sigma(x)^2$，过一个 $\exp$ 就可以得到 $\sigma(x)$ 了。

扩散模型（Diffusion Model）

简述

这里讲的是最基本的扩散模型 DDPM (Denoising Diffusion Probabilistic Model)。

原理：用 $T (\approx 1000)$ 步去噪将一个高斯噪声逐步变成清晰图像。

对比 VAE，VAE 只有一个隐变量，而 DDPM 就可以理解为有很多层隐变量。这个去噪过程会将随机高斯噪声逐步变清晰，从完全噪声开始逐渐出现轮廓，最后变得清晰。

VAE 只有一层隐变量也导致了其性能有瓶颈，实际上 VAE 训练出来的图像都比较模糊（因为信息被压缩到 $\mathbb{R}^d$ 上了），但 DDPM 生成的就较为清楚。但是相应地，DDPM 对算力的消耗就相当巨大了（生成一张图需要走 $T$ 步）。

我们的训练目标显然还是最大化对数似然 $\max_{\theta} \log p_{\theta}(x_0)$，但是

$$\begin{aligned} p_{\theta}(x_0) &= \int p_{\theta}(x_0,x_{1:T})\mathrm{d} x_{1:T} \\ &= \int p(x_T) \prod_{t \in [T]} p_{\theta}(x_{t-1}\mid x_t) \mathrm{d} x_{1:T} \end{aligned}$$

这个积分同样是 intractable 的。

用 EM 呢？在 E-step 中需要后验 $\displaystyle p_\theta(x_{1:T}\mid x_0) = \frac{p_{\theta}(x_{0:T})}{p_{\theta}(x_0)}$，同样是 intractable 的。

所以类似 VAE，引入变分分布 $q(x_{1:T}\mid x_0)$ 来近似 $p_{\theta}(x_{1:T}\mid x_0)$，于是

$$\mathrm{ELBO} = \log p_{\theta}(x_0) - \mathrm{KL}(q(x_{1:T}\mid x_0)\parallel p_{\theta}(x_{1:T}\mid x_0))$$

模型示意图如下：

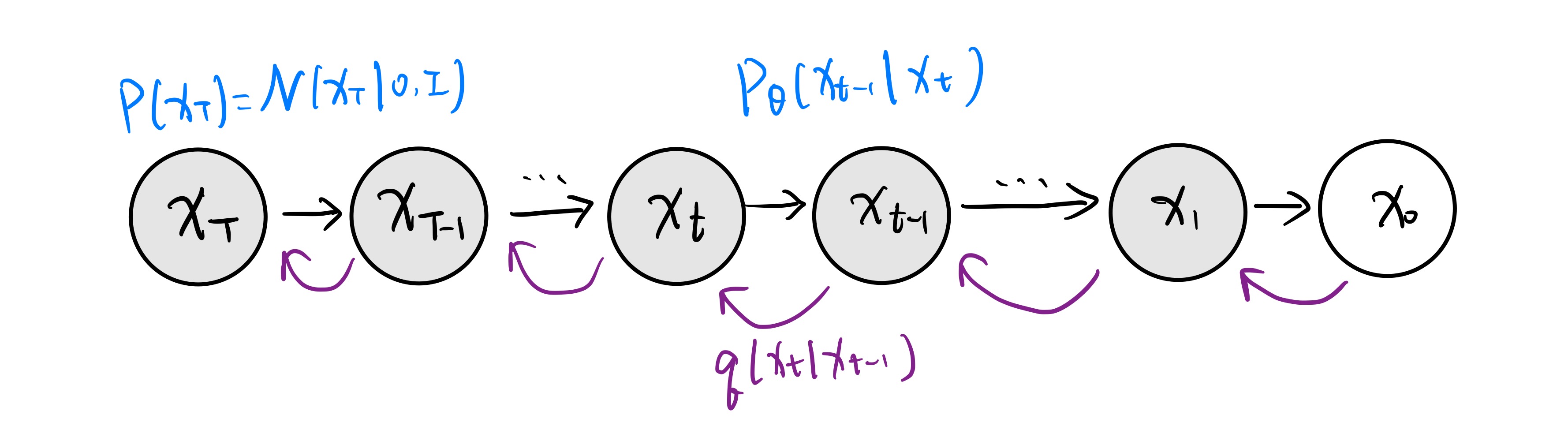
前向过程

问题在于用什么样的 $q$。

先将其 factorize：

$$q(x_{1:T}\mid x_0) = q(x_T\mid x_{T-1}) \cdots q(x_1\mid x_0)$$

可以将其称为前向的“扩散”过程。因为我们相当于是每一步都在给图像加噪声，直到变成完全的高斯噪声为止。

$t$ 增大是前向，$t$ 减小是反向。前向过程是加噪，反向过程就是去噪生成图片。

将 $q(x_t\mid x_{t-1})$ 建模成

$$q(x_t\mid x_{t-1}) = \mathcal{N}(x_t\mid \sqrt{\alpha_t} x_{t-1}, (1-\alpha_t)I)$$

均值肯定是要与 $x_{t-1}$ 有关的，不过由于到了最后要变成 $\mathcal{N}(0,I)$，所以乘上一个 $\sqrt{\alpha_t}$。这个 $\alpha_t$ 为超参数，称为 noise scheduler，控制每一步加噪声的强度。$\alpha_t$ 随着 $t$ 增大而减小。

这个形式不是随便设计的，考虑利用重参数化技巧重写 $x_t$：

$$\begin{aligned} x_t &= \sqrt{\alpha_t} x_{t-1} + \sqrt{1 - \alpha_t} \varepsilon_{t-1},&\varepsilon_{t-1} \sim \mathcal{N}(0,I)\\ &= \sqrt{\alpha_t}(\sqrt{\alpha_{t-1}}x_{t-2} + \sqrt{1 - \alpha_{t-1}}\varepsilon_{t-2}) + \sqrt{1 - \alpha_t}\varepsilon_{t-1}\\ &= \sqrt{\alpha_t \alpha_{t-1}}x_{t-2} + \sqrt{\alpha_t - \alpha_t \alpha_{t-1}}\varepsilon_{t-2} + \sqrt{1 - \alpha_t} \varepsilon_{t-1} \end{aligned}$$

考虑后两项

$$\sqrt{\alpha_t - \alpha_t \alpha_{t-1}}\varepsilon_{t-2} + \sqrt{1 - \alpha_t}\varepsilon_{t-1} \sim \mathcal{N}(0, (1 - \alpha_t \alpha_{t-1})I)$$

事实上就是将这两个高斯的 $\varepsilon$ 合并为 $\sqrt{1 - \alpha_t \alpha_{t-1}}\cdot \overline{\varepsilon}_{t-2}$，这一步也是重参数化技巧。于是可以归纳证明：

$$x_t = \sqrt{\overline{\alpha}_t}x_0 + \sqrt{1 - \overline{\alpha}_t}\cdot \varepsilon,\qquad \overline{\alpha}_t = \prod_{i \in [t]}\alpha_i$$

就可以得到简洁的形式

$$q(x_t\mid x_0) = \mathcal{N}(x_t\mid \sqrt{\overline{\alpha}_t}x_0, (1-\overline{\alpha}_t)I)$$

这就使得，如果我们想要获得中间的某步隐变量 $x_t$，就不需要一步步计算了，只需要一步到位，这就大大加速了学习的过程。

当 $t = T$ 时，$\sqrt{\overline{\alpha}_t} \to 0$，$1 - \overline{\alpha}_t \to 1$，这告诉我们 $q(x_T\mid x_0) \approx \mathcal{N}(x_T\mid 0,I)$。与我们之前关于 $x_0$ 的先验是一致的，即不论什么样的 $x_0$ 最后都会变成纯的高斯噪声，这样就不用额外优化 KL 散度了。对比 VAE，我们不能保证 $q$ 输出的分布与 $z$ 的先验是一致的，所以 loss 里面才需要那一项 KL 散度。

去噪过程

仍然令 $p_{\theta}$ 为高斯：

$$p_{\theta}(x_{t-1}\mid x_t) = \mathcal{N}(x_{t-1}\mid \mu_{\theta}(x_t,t), \Sigma_{\theta}(x_t,t))$$

其中 $\mu_{\theta}$ 和 $\Sigma_{\theta}$ 为两个神经网络。

需要往网络中额外传入 $t$ 来表明当前是第几步（不同步之间的 $x_t$ 可能是相同的，不传入 $t$ 的话神经网络无法进行区分）。

这个形式也不是随便取的。为了推出这个形式，考虑写出 ELBO：

$$\begin{aligned} \mathrm{ELBO} &= \log p_{\theta}(x_0) - \mathrm{KL} \\ &= \int_{x_{1:T}}q(x_{1:T}\mid x_0) \log p_{\theta}(x_0) \mathrm{d}x_{1:T} - \int_{x_{1:T}} q(x_{1:T}\mid x_0) \frac{q(x_{1:T}\mid x_0)}{p_{\theta}(x_{1:T}\mid x_0)} \mathrm{d} x_{1:T}\\ &= \int_{x_{1:T}} q(x_{1:T}\mid x_0) \log \frac{p_{\theta}(x_{0:T})}{q(x_{1:T}\mid x_0)}\mathrm{d} x_{1:T}\\ &= \int_{x_{1:T}} q(x_{1:T}\mid x_0) \log \frac{p(x_T) \prod_{t \in [T]} p_{\theta}(x_{t-1}\mid x_t) }{\prod_{t \in [T]} q(x_t\mid x_{t-1}) }\mathrm{d} x_{1:T}\\ &= \mathbb{E}_{x_{1:T} \sim q(x_{1:T}\mid x_0)}\left[ \log p(x_T) + \sum_{t \in [T]}\log \frac{p_{\theta}(x_{t-1}\mid x_t)}{q(x_t\mid x_{t-1})} \right] \end{aligned}$$

但是问题在于，后面那项不是两个高斯分布之间的 KL 散度，如果是的话就有非常漂亮的闭式解，但这个不是：二者的变量不匹配，分子是 $x_{t-1}$ 而分母是 $x_t$。如果说我们能把下面的 $q$ 变成形如 $q(x_{t-1}\mid x_t)$ 就好了。利用贝叶斯公式

$$q(x_{t-1}\mid x_t) = \frac{q(x_t\mid x_{t-1})\cdot q(x_{t-1})}{q(x_t)}$$

我们知道 $q(x_t\mid x_{t-1})$ 但是不知道 $q(x_t)$ 和 $q(x_{t-1})$，仍然 intractable。

怎么解决呢？DDPM 中最漂亮的观察：$q(x_{t-1}\mid x_{t})$ 是 intractable 的，但是 $q(x_t\mid x_{t-1},x_0)$ 是 tractable 的！

还是使用贝叶斯：

$$q(x_{t-1}\mid x_t,x_0) = q(x_t\mid x_{t-1},x_0) \frac{q(x_{t-1}\mid x_0)}{q(x_t\mid x_0)}$$

事实上已知 $x_{t-1}$ 的话 $x_t$ 与 $x_0$ 是独立的，所以 $q(x_t\mid x_{t-1},x_0)$ 就是 $q(x_t\mid x_{t-1})$，我们已经推导过了，而 $q(x_t\mid x_0)$ 我们也是知道的。那么接下来开算就完了：

$$\begin{aligned} q(x_{t-1}\mid x_t,x_0) &= q(x_t\mid x_{t-1},x_0) \frac{q(x_{t-1}\mid x_0)}{q(x_t\mid x_0)} \\ &= \frac{\frac{1}{(2\pi)^{\frac{d}{2}}(1-\alpha_t)^{\frac{d}{2}}}\cdot \exp\left( - \frac{\left\| x_t - \sqrt{\alpha_t}x_{t-1} \right\|^{2}}{2(1-\alpha_t)} \right) \cdot \frac{1}{(2\pi)^{\frac{d}{2}}(1-\sqrt{\overline{\alpha}_{t-1}})^{\frac{d}{2}}} \cdot \exp\left( -\frac{\left\| x_{t-1} - \sqrt{\overline{\alpha}_{t-1}} x_0 \right\|^{2}}{2(1 - \overline{\alpha}_{t-1})} \right) }{\frac{1}{(2\pi)^{\frac{d}{2}}(1-\sqrt{\overline{\alpha}_t})^{\frac{d}{2}}}\cdot \exp\left( -\frac{\left\| x_t - \sqrt{\overline{\alpha}_t} x_0 \right\|^{2}}{2(1 - \overline{\alpha}_t)} \right) }\\ &\cdots\\ &= \frac{\exp\left( -\frac{1}{2}\left( \left( \frac{\alpha_t}{1-\alpha_t}+\frac{1}{1 - \overline{\alpha}_{t-1}} \right) \left\| x_{t-1} \right\|^{2} - \left( \frac{2\sqrt{\alpha_t} x_t^T}{1 - \alpha_t} + \frac{2\sqrt{\overline{\alpha}_{t-1}}x_0^T}{1 - \overline{\alpha}_{t-1}}\right) x_{t-1} + C(x_0,x_t) \right) \right)}{(2\pi)^{\frac{d}{2}}\left[ \frac{(1-\alpha_t)(1 - \overline{\alpha}_{t-1})}{1 - \overline{\alpha}_t} \right]^{\frac{d}{2}} } \end{aligned}$$

我们需要让他是一个高斯的形式，所以需要凑出 $x_{t-1}$ 减去某个均值的平方。用配方法。

先化简一下二次项系数

$$\begin{aligned} \frac{\alpha_t}{1-\alpha_t} + \frac{1}{1 - \overline{\alpha}_{t-1}} &= \frac{\alpha_t - \alpha_t\overline \alpha_{t-1} + 1 - \alpha_t}{(1 - \alpha_t)(1 - \overline\alpha_{t-1})} \\ &= \frac{1 - \overline \alpha_t}{(1 - \alpha_t)(1 - \overline\alpha_{t-1})} \end{aligned}$$

发现这个东西和分母上的形式很相似，这是好的，指导着我们其倒数应该就是所谓方差的形式。

经过复杂计算，得到

$$\frac{1}{(2\pi)^{\frac{d}{2}}\left[ \frac{(1-\alpha_t)(1 - \overline{\alpha}_{t-1})}{1 - \overline{\alpha}_t} \right]^{\frac{d}{2}}}\cdot \exp\left( - \frac{\left\| x_{t-1} - \left( \frac{\sqrt{\alpha_t}(1 - \overline \alpha_{t-1})}{1 - \overline \alpha_t} x_t + \frac{\sqrt{\overline \alpha_{t-1}}(1 - \alpha_t)}{1 - \overline \alpha_t}x_0 \right) \right\|^{2}}{2 \cdot \frac{(1-\alpha_t)(1 - \overline{\alpha}_{t-1})}{1 - \overline{\alpha}_t}} \right)$$

于是

$$q(x_{t-1}\mid x_t,x_0) = \mathcal{N}\left( \frac{\sqrt{\alpha_t}(1 - \overline \alpha_{t-1})}{1 - \overline \alpha_t} x_t + \frac{\sqrt{\overline \alpha_{t-1}}(1 - \alpha_t)}{1 - \overline \alpha_t}x_0, \frac{(1-\alpha_t)(1 - \overline{\alpha}_{t-1})}{1 - \overline{\alpha}_t}I \right)$$

回顾之前的 $x_t$ 与 $x_0$ 之间关系的式子，利用重参数化技巧：

$$x_t = \sqrt{\overline \alpha_t}x_0 + \sqrt{1 - \overline \alpha_t}\cdot \varepsilon_t$$

可以将 $x_0$ 表示为

$$x_0 = \frac{x_t - \sqrt{1 - \overline \alpha_t}\varepsilon_t}{\sqrt{\overline \alpha_t}}$$

那么将其代入上面的均值最终可以化简得到

$$\frac{1}{\sqrt{\alpha_t}}\left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \overline \alpha_t}}\varepsilon_t \right)$$

此时 $q(x_{t-1}\mid x_t,x_0)$ 的表达式就只包含 $x_t$ 和 $\varepsilon_t$ 了：

$$q(x_{t-1}\mid x_t,x_0) = \mathcal{N}\left( \frac{1}{\sqrt{\alpha_t}}\left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \overline \alpha_t}}\varepsilon_t \right) , \frac{(1-\alpha_t)(1 - \overline{\alpha}_{t-1})}{1 - \overline{\alpha}_t}I \right)$$

回过头来看 ELBO 的式子，我们就需要想办法凑 $q(x_{t-1})$ 了来弄出 KL 散度了：

$$\begin{aligned} \mathrm{ELBO} &= \mathbb{E}_{x_{1:T} \sim q(x_{1:T}\mid x_0)}\left[ \log p(x_T) + \sum_{t \in [T]}\log \frac{p_{\theta}(x_{t-1}\mid x_t)}{q(x_t\mid x_{t-1})} \right] \\ &= \mathbb{E}_{x_{1:T} \sim q(x_{1:T}\mid x_0)}\left[ \log p(x_T) + \log \frac{p_{\theta}(x_0\mid x_1)}{q(x_1\mid x_0)} + \sum_{t=2}^T \log\frac{p_{\theta}(x_{t-1}\mid x_t)}{q(x_{t-1}\mid x_t,x_0)}\cdot \frac{q(x_{t-1}\mid x_0)}{q(x_t\mid x_0)}\right] \\ &= \mathbb{E}_{x_{1:T} \sim q(x_{1:T}\mid x_0)}\left[ \log \frac{p(x_T)}{q(x_T\mid x_0)} + \log p_{\theta} (x_0\mid x_1) + \sum_{t=2}^T \log \frac{p_{\theta}(x_{t-1}\mid x_t)}{q(x_{t-1}\mid x_t,x_0)} \right] \end{aligned}$$

注意到 $\displaystyle \log \frac{p(x_T)}{q(x_T\mid x_0)}\approx 0$，可以忽略。$\displaystyle \log p_{\theta} (x_0\mid x_1)$ 稍微麻烦一些，原论文单独对其进行了建模，但实际上是不必要的，实验证明可以融入第三项，视为一个特例。所以我们只需要考虑第三项。

符号反转一下（$\log$ 里面分子分母颠倒），变为

$$\int_{x_{1:T}} q(x_{1:T}\mid x_0)\cdot \log \frac{q(x_{t-1}\mid x_t,x_0)}{p_{\theta}(x_{t-1}\mid x_t)}\mathrm{d} x_{1:T}$$

将 $x_t,x_{t-1}$ 以外的无关项积分掉后，

$$\int_{x_t}\int_{x_{t-1}} q(x_{t-1},x_t\mid x_0)\log \frac{q(x_{t-1}\mid x_t,x_0)}{p_{\theta}(x_{t-1}\mid x_t)} \mathrm{d} x_{t-1} \mathrm{d}x_t$$

然后把 $q(x_{t-1},x_t\mid x_0)$ 拆成 $q(x_{t-1}\mid x_t,x_0)\cdot q(x_t\mid x_0)$，并将对 $x_t$ 的积分拿到最外面：

$$\int_{x_t} q(x_t\mid x_0)\int_{x_{t-1}} q(x_{t-1}\mid x_t,x_0) \log \frac{q(x_{t-1}\mid x_t,x_0)}{p_{\theta}(x_{t-1},x_t)}\mathrm{d}x_{t-1}\mathrm{d}x_t$$

KL 散度的形式这就出来了！

$$\mathbb{E}_{x_t \sim q(x_t\mid x_0)}\left[ \mathrm{KL}\left( q(x_{t-1}\mid x_t,x_0) \parallel p_{\theta}(x_{t-1}\mid x_t) \right) \right]$$

同时在这里，注意到关于 $x_t$ 求期望也可以通过重参数化的技巧等价为关于 $\varepsilon_t \sim \mathcal{N}(0,I)$ 求期望。原因还是因为这个式子：$x_t = \sqrt{\overline \alpha_t}x_0 + \sqrt{1 - \overline \alpha_t}\cdot \varepsilon_t$，二者是双射关系。

结论：两个高斯分布的 KL 散度

给定 $\mathcal{N}(\mu_1,\Sigma_1), \mathcal{N}(\mu_2,\Sigma_2)$，其 KL 散度为

$$\mathrm{KL}(\cdot \parallel \cdot ) = -\frac{1}{2}\log \frac{|\Sigma_2|}{|\Sigma_1|} - \frac{d}{2} + \frac{1}{2}\operatorname{tr}\left( \Sigma_2^{-1}\Sigma_1 \right) + \frac{1}{2}(\mu_1-\mu_2)^T \Sigma_2^{-1}(\mu_1-\mu_2)$$

不过先不要急。我们之前是令 $p_{\theta}(x_{t-1}\mid x_t) = \mathcal{N}(x_{t-1}\mid \mu_{\theta}(x_t,t), \Sigma_{\theta}(x_t,t))$，均值和方差都由神经网络来估计。但是我们既然已经知道 $q(x_{t-1}\mid x_t,x_0)$ 的均值为 $\displaystyle \frac{1}{\sqrt{\alpha_t}}\left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \overline \alpha_t}}\varepsilon_t \right)$，就可以对 $p$ 的形式进行重参数化，令为

$$\frac{1}{\sqrt{\alpha_t}}\left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \overline \alpha_t}}\varepsilon_{\theta}(x_t,t) \right)$$

这样将模型预测目标从直接估计均值转化为预测噪声，可以简化优化目标并提高训练稳定性。

同时，$\Sigma$ 也不由神经网络预测了，而是直接令为定值（可以简化计算，也可以减少模型复杂度，实验中证明也有效）。一般取 $\sigma_t^2 = 1 - \alpha_t$。即

$$p_{\theta}(x_{t-1}\mid x_t) = \mathcal{N}\left(\frac{1}{\sqrt{\alpha_t}}\left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \overline \alpha_t}}\varepsilon_{\theta}(x_t,t) \right) , (1 - \alpha_t)I \right)$$

这个 $\varepsilon_{\theta}(x_t,t)$ 其实就是用神经网络来预测噪声。

在这样的假设下，KL 散度的式子中只有最后一项不是常数，可以推导出其为

$$L_t = \frac{(1 - \alpha_t)^{2}}{2 \sigma_t^{2} \alpha_t(1 - \overline \alpha_t)} \left\| \varepsilon_t - \varepsilon_{\theta}(x_t,t) \right\|^{2}$$

最终优化形式（注意求期望的对象从 $x_t$ 等价变换到了 $\varepsilon_t$）

$$\mathbb{E}_{\varepsilon_t \sim \mathcal{N}(0,I)}\left[ \frac{(1 - \alpha_t)^{2}}{2 \sigma_t^{2} \alpha_t(1 - \overline \alpha_t)} \left\| \varepsilon_t - \varepsilon_{\theta}(x_t,t) \right\|^{2} \right]$$

DDPM 最终形式

我们在训练的时候，肯定是会对不同的 $t$ 求 $L_t$ 的，相应地权重 $\displaystyle \frac{(1 - \alpha_t)^{2}}{2 \sigma_t^{2} \alpha_t(1 - \overline \alpha_t)}$ 会变化，但是实验中发现把这个权重忽略掉后效果会更好。所以其实整个 DDPM 的损失函数形式就是

$$\mathbb{E}_{x_0,\varepsilon_t \sim \mathcal{N}(0,I),t \sim \mathrm{Uniform}[1,T]}\left[ \left\| \varepsilon_t - \varepsilon_{\theta}(x_t,t) \right\|^{2} \right]$$

DDPM 的魅力就在于，以非常复杂的推导最后推出了一个非常简洁的结果。

所以训练 DDPM 是可以并行的。

$\varepsilon_{\theta}(x_t,t)$ 的输出与输入维度相同，本质上是对当前步添加的噪声进行预测，一般使用 U-Net 架构（本文不细讨 U-Net 的架构细节）。

但是用 DDPM 生成图片是不能并行的，只能从一个纯高斯噪声出发，然后用 $\varepsilon_{\theta}$ 计算 $T$ 次噪声，一步步降噪输出最终结果，伪代码如下：

$$\begin{array}{ll} 1 & x_T \sim \mathcal{N}(0,I) \\ 2 & \textbf{for } t\gets T\textbf{ to }1\textbf{ do}\\ 3 & \qquad \textbf{if } t=1 \textbf{ then }\\ 4& \qquad\qquad z=0 \\ 5& \qquad \textbf{else}\\ 6& \qquad\qquad z \sim \mathcal{N}(0,I)\\ 7& \qquad \textbf{endif}\\ 8& \qquad x_{t-1} = \dfrac{1}{\sqrt{\alpha_t}}\left( x_t - \dfrac{1 - \alpha_t}{\sqrt{1 - \overline \alpha_t}}\varepsilon_{\theta}(x_t,t) \right) + \sigma_t\cdot z \\ 9 & \textbf{end for}\\ 10 & \textbf{return }x_0 \end{array}$$

其中 $z$ 是为了添加随机噪声。

在 DDPM 的基础上有很多工作对其进行改进，在此不表。

完结撒花~