24秋机器学习笔记-07-高斯过程

本文主要涉及高斯过程相关的推导以及应用。
一键回城。

作者的概率统计知识相当菜，在课后费了好大劲才搞懂这一节的内容，如有错误欢迎随时指出，吾必当感激不尽！

多元高斯分布（Multivariate Gaussian Distribution）

考虑多元高斯分布

$$\mathcal{N}(x\mid \mu,\Sigma)$$

$\mu \in \mathbb{R}^d$ 为均值，$\Sigma \in \mathbb{R}^{d\times d}$ 为协方差矩阵。$\Sigma_{ij} = \operatorname{Cov}(x_i,x_j) = \mathbb{E}[(x_i - \mu_i)(x_j-\mu_j)] = \mathbb{E}[x_i x_j] - \mathbb{E}[x_i]\mathbb{E}[x_j]$。

概率密度函数：

$$\frac{1}{(2\pi)^{\frac{d}{2}}} \frac{1}{|\Sigma|^{\frac{1}{2}}} \exp\left( -\frac{1}{2}(x-\mu)^T \Sigma^{-1}(x-\mu) \right)$$

$d=1$ 的时候，$\mu\in \mathbb{R}$，$\Sigma = \sigma^{2}$，概率密度函数为

$$\mathcal{N}(x\mid \mu,\sigma^{2}) = \frac{1}{\sqrt{2\pi\sigma^{2}}} \exp\left( -\frac{1}{2\sigma^{2}}(x-\mu)^{2} \right)$$

与我们学过的一维的形式是相同的。

当 $\Sigma$ 为对角阵的时候，说明各维度之间互相独立，联合分布就可以拆开：

$$\mathcal{N}(x\mid \mu, \Sigma) = \prod_{n=1}^d \frac{1}{\sqrt{2\pi \sigma_i^2}}\exp\left(- \frac{(x_i-\mu_i)^{2}}{2\sigma_i^{2}} \right)$$

性质：

$$\mathbb{E}[x] = \int_X x \mathcal{N}(x\mid \mu, \Sigma) \mathrm{d}x = \mu$$

$$\operatorname{Cov}[x] = \begin{bmatrix} \operatorname{Cov}(x_1,x_1) & \operatorname{Cov}(x_1,x_2) & \cdots & \operatorname{Cov}(x_1,x_d) \\ \vdots & \vdots & & \vdots \\ \operatorname{Cov}(x_d,x_1) & \operatorname{Cov}(x_d,x_2) & \cdots & \operatorname{Cov}(x_d,x_d) \\\end{bmatrix} = \mathbb{E}[x x^T] - \mathbb{E}[x]\mathbb{E}[x^T] = \Sigma$$

PRML 2.3

随机过程（Stochastic Process）

定义：A collection of (infinitely) random variables along an index set.

Index set 可以为 $\mathbb{N},\mathbb{R},\mathbb{R}^d$。其可以在描述时间，但更一般性的描述下其也不一定是时间。

考虑 index $x_i$，$x_i$ 对应的随机变量采样得到 $y_i$。当有无限多组 $\{(x_i,y_i)\}$ 时候可以确定一个函数 $y(x)$ 的分布，每次采样会得到一个确定的函数 $y(x)$。

为了确定一个随机过程，我们只需要确定其包含的所有随机变量的联合分布（joint distribution）注意，这些随机变量大概率是不独立的。

例 1：伯努利过程（扔硬币）

$\{y_1,y_2, \cdots ,y_n\}$，$y_i \sim \text{Ber}(p)$
Joint distribution: $P(y_1), \cdots ,P(y_n) = P(y_1)P(y_2)\cdots P(y_n)$

接下来看一个有意思些的

例 2：Markov 随机过程

$\{y_1,y_2, \cdots ,y_T\}$，一般认为建立在时间序列上。$P(y_{t+1}\mid y_1, \cdots ,y_t) = P(y_{t+1}\mid y_t)$。

注意到 $P(y_1, \cdots ,y_T) = P(y_1)P(y_2\mid y_1)P(y_3\mid y_1,y_2)\cdots$ 是肯定对的，无论有无条件独立性的假设。

而在 Markov 过程中，$y_{t+1}$ 是与 $y_1, \cdots ,y_{t-1}$ 无关的，而只与 $y_t$ 有关。

所以，若有 Markov 的性质，我们就有 $P(y_1, \cdots,y_T) = P(y_1)P(y_2\mid y_1)P(y_3\mid y_2)\cdots P(y_T\mid y_{T-1})$

高斯过程（Gaussian Process）

定义与求解推导

joint distribution over any finite collection of R.V.s to be Gaussian.

考虑任意 $\forall \{x_1,x_2, \cdots ,x_n \}\subseteq X$，其中 $X$ 为标号集合，则其对应的随机变量 $\{y_1,y_2, \cdots ,y_n\}$ 为高斯过程当且仅当 $y_1, \cdots ,y_n$ 服从高斯分布。

为了确定一个高斯过程，我们可以对于每个随机变量 $y_i$，确定其 $\mu_i$，以及对于每个 $i,j$ 对，确定 $\Sigma_{ij}$。但是如果随机变量的个数很多，而且再考虑往里面添加新的随机变量的话，需要确定的参数数量就会呈指数级爆炸。所以我们希望有一种 consistent 的方式来进行求解。

考虑求出两个函数 $m(\cdot ),k(\cdot,\cdot )$，其以随机变量 $y_i$ 对应的下标 $x_i$ 作为输入（不能以随机变量作为输入，毕竟我们就想要的是均值和协方差），分别输出 $\mu_i$ 和 $\Sigma_{ij}$。

其实这个 $k(\cdot ,\cdot )$ 就是核函数，考虑到核函数的含义是给出两个向量的相似度，在这里就可以变相地说明 $y_i$ 和 $y_j$ 的相似程度——下标 $x_i,x_j$ 越接近，$y_i,y_j$ 越相关，这也是很符合直觉的（geometric meaning）。

有了这两个函数之后，我们就可以将一个高斯过程写成

$$y(x) \sim \operatorname{GP}(m(x), k(x,x'))$$

一般而言，我们都直接令 $m(x) = 0$（回忆贝叶斯角度下的线性回归），在无关于 $y$ 的先验知识下令均值为 $0$ 是很符合 Occam’s Razar 原理的。

同时，$\Sigma$ 应该是正定的。合法的核函数已经满足其半正定性。如果出现了有特征值为 $0$ 的情况，可以通过添加 $\lambda I$ 噪声来进行解决。

考虑求解 $k$。我们其实一般使用 RBF kernel：

$$k(x_i,x_j) = \exp\left( - \frac{\left\| x_i - x_j \right\|^{2}}{2 l^2} \right)$$

令 $K$ 为 $n$ 个训练点 $x_1, \cdots ,x_n$ 对应的 Gram 矩阵，其中 $K_{ij} = k(x_i,x_j)$，$K \in R^{n\times n}$，然后令 $y := [y_1, \cdots ,y_n]^T$ 为 $n$ 维随机变量。

则我们有 $P(y) = \mathcal{N}(y\mid 0,K)$，其为训练数据的标签的联合分布。

但是光有这个没有用，对于训练数据，我们是知道 GT 的，即知道每个 $y_i$ 分别是什么，我们更需要的是给定一个新的测试点 $x^*$，求出 $P(y^*\mid y)$。

先考虑求出 $y^*$ 与 $y$ 的联合分布。这还是比较容易的：

$$P\left(\begin{bmatrix} y^* \\ y \\\end{bmatrix} \right) = \mathcal{N}\left(\begin{bmatrix} y^* \\ y \\\end{bmatrix} \mid 0, \begin{bmatrix} k(x^*,x^*) & k(x^*)^T \\ k(x^*) & K \\\end{bmatrix}\right)$$

其中，$k(x^*) = [k(x^*,x_1), \cdots ,k(x^*,x_n)]^T$。但这并不够，我们要的是条件分布而不是联合分布。

根据高斯分布相关性质，不加证明地，我们知道，这个条件分布仍是高斯分布：

$$P(y^*\mid y) = \mathcal{N}(y^*\mid \mu^*, \Sigma^*)$$

这意味着我们只需要确定 $\mu^*$ 和 $\Sigma^*$ 即可。接下来利用高斯分布的一些结论（同样不加证明地）：

Standard Conclusions from Gaussian

对于一个随机变量

$$X = \begin{bmatrix} x_a \\ x_b \\\end{bmatrix} \sim \mathcal{N}\left( \begin{bmatrix} \mu_a \\ \mu_b \\\end{bmatrix}, \begin{bmatrix} \Sigma_{aa} & \Sigma_{ab} \\ \Sigma_{ba} & \Sigma_{bb} \\\end{bmatrix} \right)$$

其中 $x_a \in \mathbb{R}^a$，$x_b \in \mathbb{R}^b$，即把 $a+b$ 维拆开来。

1. 边缘化（marginalization）：

   $$\begin{aligned} x_a &\sim \mathcal{N}(\mu_a, \Sigma_{aa}) \\ x_b &\sim \mathcal{N}(\mu_b, \Sigma_{bb}) \end{aligned}$$

2. 条件分布：

   $$P(x_a\mid x_b) = \mathcal{N}(x_a\mid \mu_{a\mid b}, \Sigma_{a\mid b})$$

   其中

   $$\begin{aligned} \mu_{a\mid b} &= \mu_a + \Sigma_{ab}\Sigma_{bb}^{-1}(x_b - \mu_b) \\ \Sigma_{a\mid b} &= \Sigma_{aa} - \Sigma_{ab}\Sigma_{bb}^{-1}\Sigma_{ba} \end{aligned}$$

   这个式子会在之后的部分反复用到。

补充：张老师关于该式子物理含义的理解

考虑 $\mu_{a\mid b}$：该式子在描述在标准化意义下，$x_b$ 偏离其均值有多大。除以 $\Sigma_{bb}$ 相当于在做标准化，而 $\Sigma_{ab}$ 的含义为 $x_a$ 与 $x_b$ 倾向于一起怎么样变动。$x_b$ 偏离均值越大，相应地对 $\mu_a$ 影响也会越大。

对于 $\Sigma_{ab}$：确定了 $x_b$ 之后，$x_a$ 的“不确定度”就会减小，所以 $\Sigma_{aa}$ 后面跟着的是减号。减小的程度与 $x_a,x_b$ 的相关程度也是成正比的——越相关，确定 $x_b$ 后就“越能确定” $x_a$，但还是会反比于 $x_b$ 的“不确定度”——若 $x_b$ 本身不确定程度就很大，那么观察到后对 $x_a$ 的影响也就应该没那么大。

对其有直觉上的理解可以方便记忆。

那么直接套这个结论，就可以很快求出我们要的结果了：

$$\begin{aligned} \mu^* &= k(x^*)^T K^{-1}y \\ \Sigma^* &= k(x^*,x^*) - k(x^*)^T K^{-1} k(x^*) \end{aligned}$$

有没有发现什么问题？$K$ 不一定是可逆的。回忆之前学过的知识，遇到这种情况我们一般会想办法弄成 $(K + \lambda I)$ 的形式，这样就一定可以求逆了。在线性回归的时候，我们添加了一个正则化项让这个形式 make sense 了，而此时我们也需要想一个让这个形式变得合理的办法。

Noise Setting

在之前，我们是假设观测到了 $y$ 的 ground truth (GT)。现在我们假设 $y$ 是带有噪声的，即 $\hat{y} = y + \varepsilon$，其中 $\varepsilon \sim \mathcal{N}(0, \sigma^{2}I)$。接下来重新推导 $y^*$ 与 $\hat{y}$ 的联合分布与条件分布。

高斯分布有特别好的性质：对其做组合/线性变换后仍为高斯分布。所以 $P([y^*, \hat{y}]^T)$ 仍为高斯分布。

均值是简单的，仍是 $0$（因为添加的噪声项的均值为 $0$），而协方差矩阵就需要思考一下了：$k(x^*,x^*)$ 不变，但 $k(x^*)$ 和 $K$ 就会发生改变了，我们用协方差的定义去推导：

$$\begin{aligned} \operatorname{Cov}(y^*, \hat{y_i}) &= \mathbb{E} [y^* \hat{y_i}] - \mathbb{E}[y^*]\mathbb{E}[\hat{y_i}] \\ &= \mathbb{E}[y^* \hat{y_i}]\\ &= \mathbb{E}[y^*(y_i+\varepsilon)]\\ &= \mathbb{E}[y^* y_i] + \mathbb{E}[y^*] \mathbb{E}[\varepsilon]\\ &= \mathbb{E}[y^* y_i]\\ &= \operatorname{Cov}(y^*,y_i) + \mathbb{E}[y^*] E[y_i]\\ &= \operatorname{Cov}(y^*, y_i) = k(y^*, y_i) \end{aligned}$$

所以 $k(x^*)$ 还是不变的！接下来看 $K$：

$$\begin{aligned} \operatorname{Cov}(\hat{y_i},\hat{y_j}) &= \mathbb{E}[\hat{y_i} \hat{y_j}] - \mathbb{E}[\hat{y_i}] \mathbb{E}[\hat{y_j}] \\ &= \mathbb{E}[(y_i + \varepsilon_i)(y_j + \varepsilon_j)]\\ &= \mathbb{E}[y_i y_j] + \mathbb{E}[y_i \varepsilon_j] + \mathbb{E}[y_j \varepsilon_i] + \mathbb{E}[\varepsilon_i \varepsilon_j]\\ &= k(x_i,x_j) + \sigma^{2}1(i =j) \end{aligned}$$

所以得到结论：

$$P\left( \begin{bmatrix} y^* \\ \hat{y} \\\end{bmatrix} \right) = \mathcal{N}\left( \begin{bmatrix} y^* \\ \hat{y} \\\end{bmatrix} \mid 0,\begin{bmatrix} k(x^*,x^*) & k(x^*)^T \\ k(x^*) & \color{red}{K + \sigma^{2}I} \\\end{bmatrix} \right)$$

这正是我们想要的——所以条件分布也可以写出来了：

$$P(y^*\mid \hat{y}) = \mathcal{N}(y^*\mid k(x^*)^T(K + \sigma^{2}I)^{-1}\hat{y}, k(x^*,x^*) - k(x^*)^T (K + \sigma^{2}I)^{-1}k(x^*))$$

其可以避免数值问题，提高计算稳定性。实际应用中也都是这个形式。

高斯过程视角下的岭回归

考虑岭回归：

$$\min_w \left\{ (y_i - w^T \varphi(x_i))^{2} + \lambda w^Tw \right\}$$

假设观测到的 $y_i$ 有噪声。

从贝叶斯的视角来看，$w$ 也是随机变量，给出其先验分布：

$$w \sim \mathcal{N}(0, \sigma_w^{2}I)$$

再看看 $y_i$：

$$y_i = w^T \varphi(x_i) + \varepsilon_i$$

$\varphi(x_i)$ 为确定的值，$w$ 为随机变量，$\varepsilon_i$ 也为随机变量，所以 $y_i$ 也是随机变量！更进一步地，我们注意到 $y_i$ 也服从高斯分布（因为其为服从高斯分布的随机变量的线性组合）

所以，我们可以将 $y$ 理解成高斯过程。

推导 $y$ 对应的 $m(\cdot )$ 和 $k(\cdot ,\cdot )$ 吧。自然我们假设 $m \equiv 0$。

$$\begin{aligned} \operatorname{Cov}(y_i,y_j) &= \mathbb{E}[y_i y_j] - \mathbb{E}[y_i]\mathbb{E}[y_j] \\ &= \mathbb{E}[(w^T \varphi(x_i) + \varepsilon_i)(w^T \varphi(x_j) + \varepsilon_j)]\\ &= \mathbb{E}[\varphi(x_i)^T w w^T \varphi(x_j)] + \mathbb{E}[\varepsilon_i \varepsilon_j] \end{aligned}$$

对于 $\mathbb{E}[\varepsilon_i\varepsilon_j]$，我们知道其为 $\sigma^{2}1(i =j)$。又发现 $\operatorname{Cov}(w) = \mathbb{E}[ww^T] - \mathbb{E}[w] \mathbb{E}[w^T]$，后者均为 $0$，所以

$$\begin{aligned} \operatorname{Cov}(y_i,y_j) &= \varphi(x_i)^T \sigma_w^{2}I \varphi(x_i) \\ &= \sigma_w^{2} k(x_i,x_j) \end{aligned}$$

所以

$$y \sim \mathcal{N}(0, \sigma_w^{2}K + \sigma^{2}I)$$

套用之前的结论就可以得到，若给一个 $x^*$，要预测 $y^*$，则

$$y^*\mid y \sim \mathcal{N}(\sigma_w^{2} k(x^*)^T (\sigma_w^{2}K + \sigma^{2}I)^{-1}y, \sigma_w^{2}k(x^*,x^*) - \sigma_w^{4}k(x^*)^T(\sigma_w^{2}K + \sigma^{2}I)^{-1}k(x^*))$$

所以高斯过程可以理解成线性回归的一个 kernel 版本，就也可以使用核技巧了。（可以类比一下 SVM）

其经常可以用来在非线性的情况下做一些回归问题，这种回归称为高斯过程回归（GPR）

应用

一些小细节：

• $y^*$ 可以是一个点，也可以是一个向量（即我们一次性预测很多个点）
• 和之前学习的回归模型不同，我们得到的是关于 $y^*$ 的一个分布。我们可以用其均值直接给出输出，也可以利用方差给出一个置信区间。
• $\sigma$ 为超参数。

最常用的核函数就是 RBF 核：

$$k(x,x') = \exp\left( -\frac{\left\| x - x' \right\|^{2}}{2l^{2}} \right)$$

其中 $l$ 为 length scale，为超参数，此处不展开。

高斯过程回归（GPR）

假设下标集合为一维。并且有 $6$ 个训练样本（$\hat{y}$ 的 GT 在下图中用红点标出）。

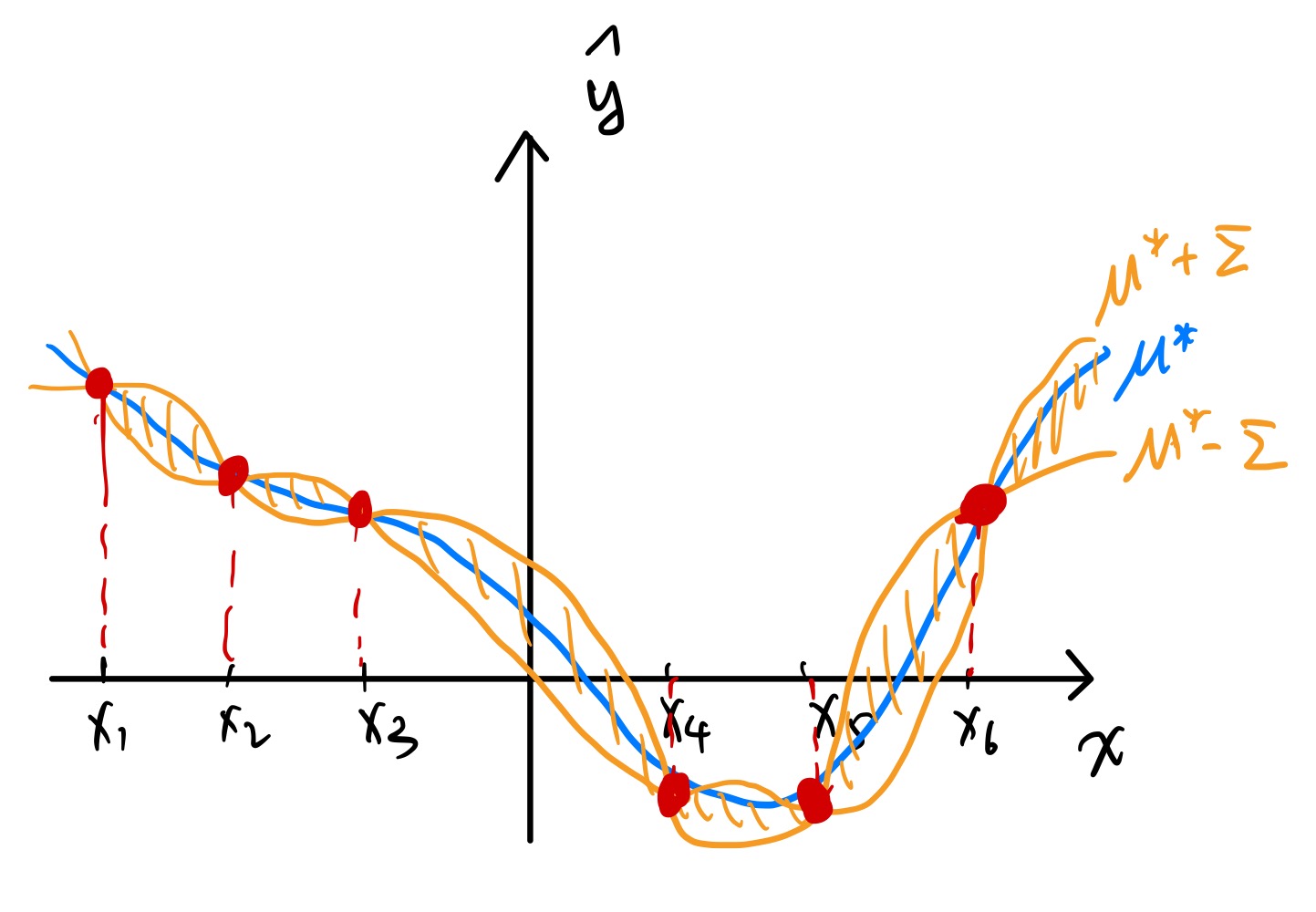
对这六个训练样本做 GPR，可以得到一条 $\mu^*$ 关于 $x^*$ 的平滑曲线（蓝色标出），然后同时也可以画出标准差的图像，在上图中可以清晰看到离训练点越近，预测结果的置信度就越高（这也是很符合直觉的）

需要注意的是，$\mu^*$ 未必穿过所有数据点。只有当 $\sigma^2 = 0$，$l\to 0$ 时，$\mu^*$ 才会恰好穿过所有数据点。

推导：令 $x^* = x_n$，$k(x^*,x^*) = 1$，且由于 $l\to 0$，$\forall x \neq x^*$ 有 $k(x^*,x) = 0$，所以 $K = I$。此时 $\mu^* = k(x^*)^T I y = y_n$。

贝叶斯优化（Bayesian Optimization, BO）

先介绍黑箱优化（black-box optimization），其目标函数是没有解析形式的，更不用提梯度了。传统的梯度下降法对于黑箱优化是无效的。

我们只能做的是，不断喂进去 $x$，然后观测其输出的 $y$。现在的目标就是在尽可能少的次数下使得 $y$ 最大化。神经网络的超参数调参就是一种典型的黑箱优化问题。

误区：可能会觉得神经网络不是可以用梯度下降优化吗？

注意我们这里讨论的是超参数，神经网络最后输出的 performance 是无法被写成超参数的解析形式的。

贝叶斯优化的流程如下：

1. 随机采样若干点，并扔进黑箱求值，得到初始的 $\{(x_i,y_i)\}$；
2. 用这些点做一个 GPR；
3. 在回归结果的基础上，利用采集函数（acquisition function）$a(x)$ 来选择新的一批点，并将这些点加入已知训练点，重新做 GPR；
4. 重复第三步直到满足某种停止条件。

采集函数扮演着非常重要的角色，常见的有如下几种：

• Expected Improvement (EI)：$a(x) = \mathbb{E}[(y(x) - y_{\max})^+]$，寻找期望意义下能给 $y_{\max}$ 带来最大改进的点。
• Upper Confidence Bound：$a(x) = \mu(x) + \kappa \sigma(x)$。和 MCTS 里面的那个很像，相当于在平衡利用（exploitation）和探索（exploration）。

超参数调整软件推荐：optuna

Acknowledgement

• https://www.cnblogs.com/stxs/p/9131046.html