24秋机器学习笔记-09-集成学习

一键回城。

概览

核心思想：将若干（弱）的模型组合在一起以获得一个强的模型。这些模型需要尽可能 diversed（因为如果都一样的话就起不到增强的效果了）

回顾偏差-方差分解：

$$\mathbb{E}_D[(f(x;D) - y)^2] = \mathbb{E}_D[(f(x,D) - \overline{f}(x))^2] + (\overline{f}(x) - y)^{2}$$

高方差低偏差的模型：树模型，神经网络；低方差高偏差的模型：线性模型。

集成学习模型一般可以分为 Bagging 和 Boosting 两类。

Bagging

Bagging 的目的是减少方差，所以被集成的模型一般为高方差低偏差的模型。

理想情况下，假设我们可以从分布 $P(D)$ 中反复采样训练集 $D$，然后令 $\displaystyle f(x) = \frac{1}{T} \sum_{t \in [T]} f(x;D_t)$。可以发现当 $T\to \infty$ 的时候 $f(x)\to \bar{f}(x)$，于是方差也会 $\to 0$。

然而，实际上我们只有一个 $D$，所以无法做到从 $P(D)$ 中反复采样。解决方案为 Bootstrap（自举）

Bootstrap

流程：

1. 从 $D$ 中有放回地抽样 $n$ 个点（为什么是有放回，因为考虑到如果是无放回的话，每次的结果都是一样的了）；
2. 重复第一步 $T$ 次，得到 $\hat{D_1},\hat{D_2}, \cdots ,\hat{D}_T$；
3. $\displaystyle \hat{f}(x) = \frac{1}{T} \sum_{t \in [T]} f(x;\hat{D}_t)$

考虑一个简单的小问题：计算一个点 $(x_i,y_i)$ 没有在 $\hat{D_t}$ 中的概率，以及当 $n\to \infty$ 时，其极限是多少。

显然

$$p = \left( 1-\frac{1}{n} \right)^n \to \frac{1}{e} \approx 36.8\% \quad(n \to \infty)$$

所以平均来看，每个 $\hat{D}_t$ 只会包含 $D$ 中 $63.2\%$ 的数据，我们可以将剩下的未被包含进去的数据作为 hold-out validation set（也叫做 out of bag set）

需要注意的是，Bootstrap 是没有理论保证的，但是经验上来看其确实能有效减小测试误差。

No model is correct, but some models are useful

随机森林（Random Forest）

其为最成功的 bagging 模型——“对于简单分类任务，必须尝试的一个模型”。

$$\begin{array}{ll} 1 & \textbf{Input. } \text{Training data }D, \text{ features }F \text{, number of trees }T \\ 2 & \textbf{Output. } \text{A model consisting of }T \text{ decision trees} \\ 3 & \textbf{Method. } \\ 4 & B \gets \text{An empty array} \\ 5 & \textbf{for } t\gets 1\textbf{ to }T\textbf{ do}\\ 6 & \qquad \text{Sample }n \text{ points }\hat{D_t}\text{ from }D \textit{ with replacement}\\ 7 & \qquad \textcolor{yellow}{\text{Sample }d' < d \text{ features }F' \text{ from } F \textit{ without replacement}} \\ 8 & \qquad \text{Build a full decision tree on } \hat{D}_t, F'\text{ (can do some prowing to minimize out-of-bag error)} \\ 9 & \textbf{end for}\\ 10 & \text{Average all decision trees to get final model} \end{array}$$

注意其强大之处来源于每棵决策树的 feature 集合也都是不同的！

简单，容易实现，非常强大。

Boosting

与 bagging 相对地，boosting 的核心在于减小偏差，所以一般选用低方差高偏差的模型，如线性模型或限制了树高的树模型。

AdaBoost

考虑做二分类问题。$D = \{(x_1,y_1), \cdots ,(x_n,y_n)\}$，$y \in \{-1,+1\}$，$x \in \mathbb{R}^d$。

输入：$D$ 以及一个弱的学习算法 $A$（例如线性模型，AdaBoost 就可以让若干个线性模型集成为一个可以做非线性分类的模型）。

1. 初始化采样权重（每一个数据点的权重）：$\displaystyle W_i^{(1)} = \overline{W_i}^{(1)} = \frac{1}{n}, i \in [n]$。
2. For $t \in [T]$：

• 用 $D$ 和 $\{W_i^{(t)}\}$ 训练得到一个模型 $f_t(x): \mathbb{R}^d\to \{-1,+1\}$。
• 计算 $f_t(x)$ 在 $D$ 上的带权分类误差（weighted classification error）$\displaystyle e_t = \sum_{i \in [n]} W_i^{(t)}1(f(x_i)\neq y_i)$
• 计算 $f_t(x)$ 的权重 $\alpha_t$：$\displaystyle \alpha_t = \frac{1}{2} \log \frac{1-e_t}{e_t}$。这个权重是在最终组合的时候的权重，$e_t$ 越大，$\alpha_t$ 越小，符合直觉。且 $e_t>0.5$ 时 $\alpha_t <0$（把一半以上的数据都预测错了，那不如直接把输出取反）
• 更新数据点的权重 $\overline{W_i}^{(t+1)} = \overline{W_i}^{(t)}\cdot \exp(-\alpha_t y_i f_t(x_i))$，归一化得到 $\displaystyle W_i^{(t+1)} = \frac{\overline{W_i}^{(t+1)}}{\sum_{j \in [n]}\overline{W_j}^{(t+1)}}$
  考虑 $\exp(-\alpha_t y_i f_t(x_i))$ 这个式子的含义：一般而言 $\alpha_t$ 为正（$e_t>0.5$ 还是比较罕见的），则这个式子就是在考虑 $y_i$ 和 $f_t(x_i)$ 是否同号。若同号，说明 $f_t$ 预测对了，则 $\exp$ 括号中的内容为负，对应着在接下来的训练中 $(x_i,y_i)$ 的权重会减小；反之若异号，则 $f_t$ 预测错误，$\exp$ 括号内为正，对应着权重会增加。事实上 $\alpha_t$ 为负的时候也不影响正确性，因为 $\alpha_t<0$ 意味着已经对模型“取反”。

3. 将 $T$ 个 $f_t(x)$ 线性地组合起来：$\displaystyle g(x) = \sum_{t \in [T]}\alpha_t f_t(x)$，$g(x)\ge 0$ 时输出 $1$，反之输出 $-1$。

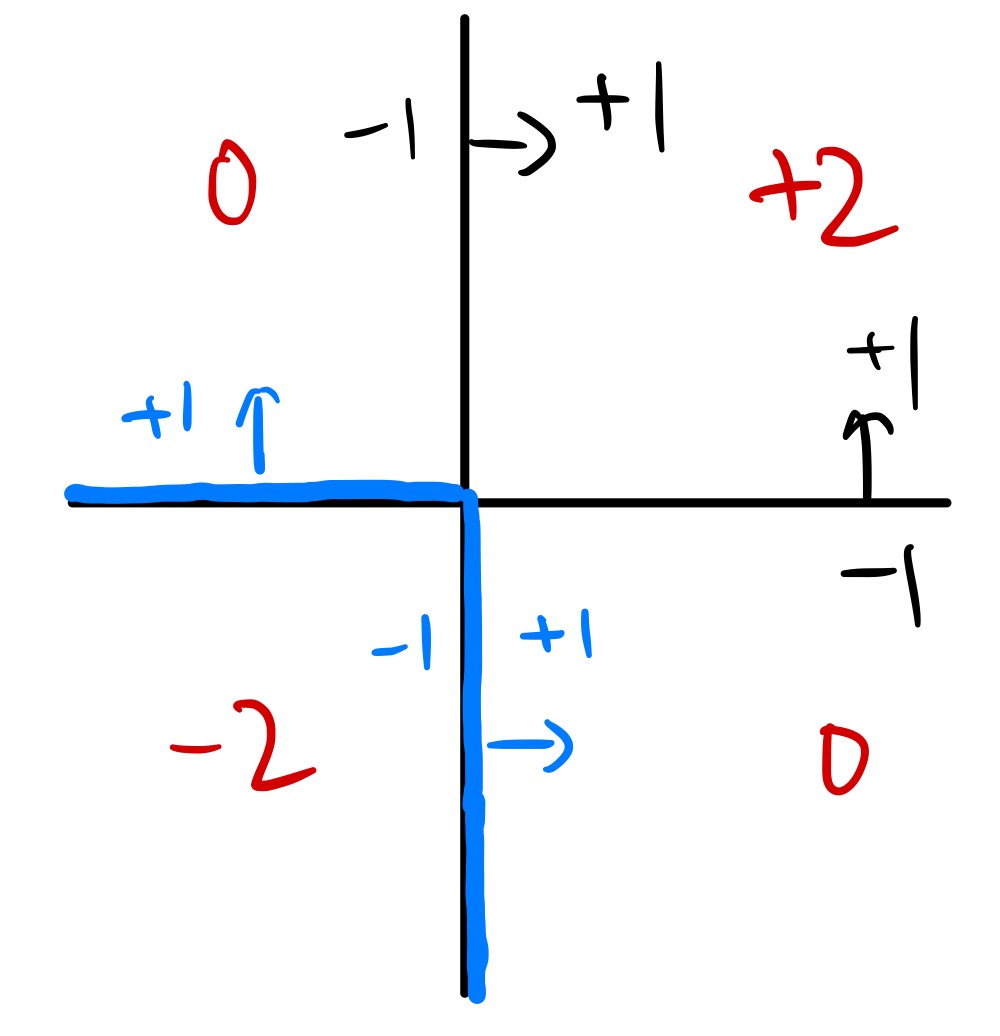
例如：如下图中，利用 AdaBoost 后得到两个分类器，分别为水平/竖直，且其权重相等，则组合后 $g$ 的输出结果为红色所示，得到的最终分隔的边界为蓝色所示，可以发现其变为非线性的了。

加性模型（Additive Model）

是 boosting 的一种通用范式。

$$g(x) = \sum_{t \in [T]} \alpha_t f_t(x)$$

定义

$$g_t(x) = \sum_{j \in [t]} \alpha_j f_j(x)$$

在第 $t$ 步，固定 $g_{t-1}(x)$，通过最小化某个损失函数来学习 $\alpha_t, f_t(x)$。该损失函数为

$$\sum_{i \in [n]}L(y_i, g_{t-1}(x_i) + \alpha_t f_t(x_i))$$

最终 $g(x) = g_T(x)$。大概含义就是，每次迭代只更新一个模型，同时计算损失函数的时候也考虑前面已经训练好了的模型。

AdaBoost 就是一种特殊的加性模型，其使用的损失函数为指数损失函数（exponential loss）$L(y,f(x)) = \exp(-yf(x))$

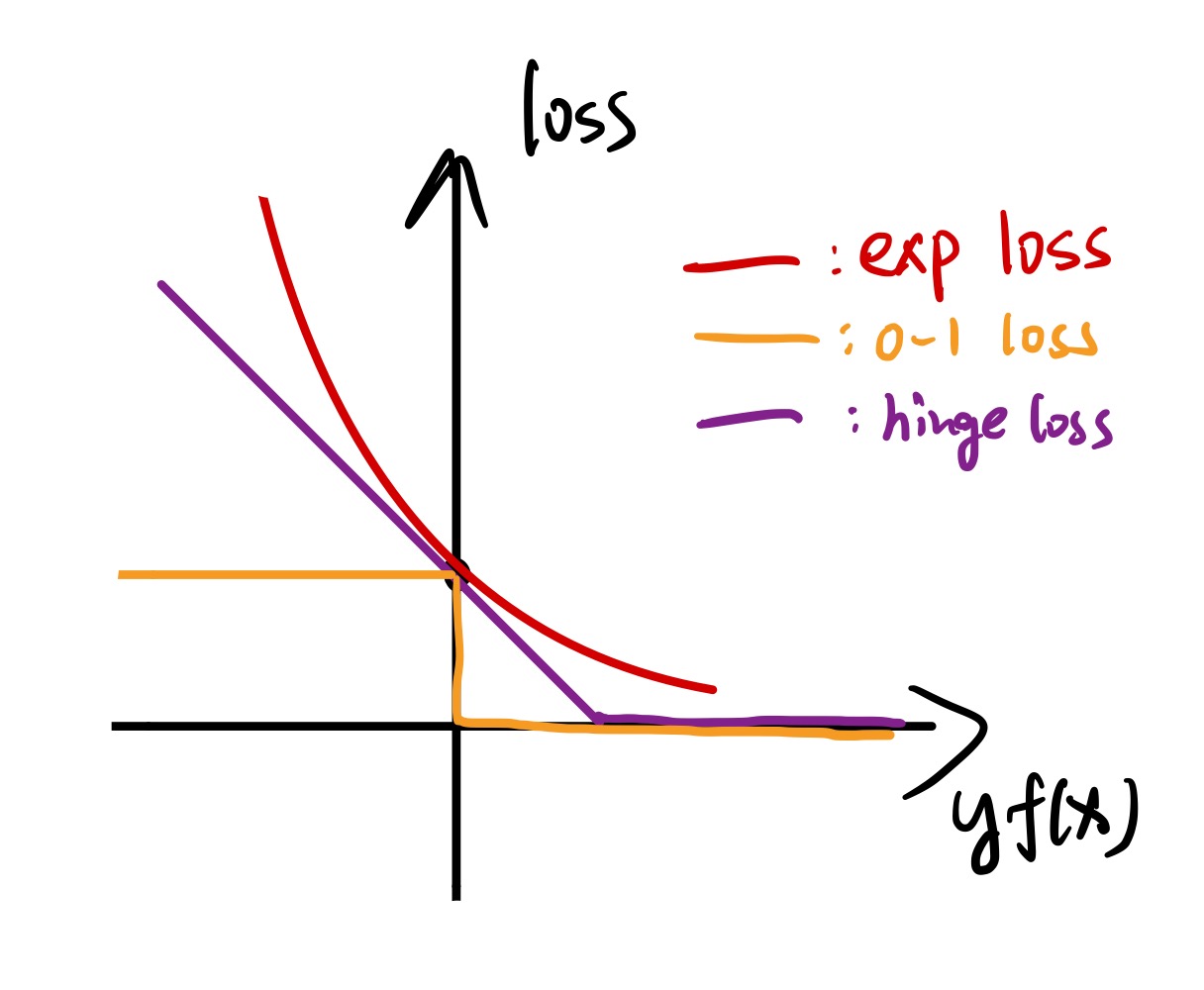
其是 hinge loss 和 0-1 loss 的替代（或者说上界），而且在 $yf(x)<0$ 的时候增长地非常快。不过在 AdaBoost 里面，由于 $yf(x)$ 的取值只有 $\pm 1$，所以损失函数的取值只可能为 $e$ 或 $1 / e$。（存疑）

AdaBoost 的推导

在第 $t$ 步的时候，我们已经有 $\displaystyle g_{t-1}(x) = \sum_{j \in [t-1]}\alpha_j f_j(x)$。

我们现在需要优化

$$\min_{\alpha_t, f_t} \sum_{i \in [n]} \exp(-y_i(g_{t-1}(x_i) + \alpha_tf_t(x_i)))$$

定义 $\overline{W_i}^{(t)}:= \exp(-y_ig_{t-1}(x_i))$，事实上这个东西就是我们刚才的那个权重：

$$\begin{aligned} \exp(-y_i g_{t-1}(x_i)) &= \prod_{j \in [t-1]} \exp(-y_i \alpha_j f_j(x_i)) \\ &= \overline{W_i}^{(t-1)} \cdot \exp(-y_i \alpha_{t-1}f_{t-1}(x_i)) \end{aligned}$$

可以发现和之前的定义是一致的。原来的最优化问题可以拆成：

$$\min_{\alpha_t} \min_{f_t} \sum_{i \in [n]} \overline{W_i}^{(t)} \cdot \exp(-y_i \alpha_t f_t(x))$$

Claim：归一化后的 $W_i^{(t)}$ 与 $\overline{W_i}^{(t)}$ 只相差常数，所以在最优化问题中可以用前者替换掉后者：

$$\min_{\alpha_t} \min_{f_t} \sum_{i \in [n]} W_i^{(t)} \cdot \exp(-y_i \alpha_t f_t(x))$$

现在的策略：因为 $\alpha_t$ 只是个标量（可以称为温度），不影响 $f_t$ 的训练，所以先固定 $\alpha_t$，优化 $f_t$（但是还是很难）。所以在 AdaBoost 中，我们进行了简化，即用 $f_t$ 自己的损失函数和采样权重 $W_i^{(t)}$ 来训练，实际上也大差不差。

固定了 $f_t$ 后，接下来要做的就只有优化 $\alpha_t$ 了。按照 $y_i$ 是否等于 $f_t(x_i)$ 将数据集分为两部分，上述优化问题等价于

$$\min_{\alpha_t} \sum_{y_i = f_t(x_i)} W_i^{(t)} \exp(-\alpha_t) + \sum_{y_i\neq f_t(x_i)} W_i^{(t)}\exp(\alpha_t)$$

进行添项减项：

$$\sum_{y_i = f_t(x_i)} W_i^{(t)} \exp(-\alpha_t) + \sum_{y_i\neq f_t(x_i)} W_i^{(t)}\exp(-\alpha_t) + \sum_{y_i\neq f_t(x_i)} W_i^{(t)}\exp(\alpha_t) - \sum_{y_i\neq f_t(x_i)} W_i^{(t)}\exp(-\alpha_t)$$

将前面两项合并，发现是 $\displaystyle \sum_{i \in [n]} W_i^{(t)}\exp(-\alpha_t)$，而 $\sum W_i^{(t)} = 1$，所以前两项就剩个 $\exp(-\alpha_t)$。

后面两项为 $\displaystyle \textcolor{yellow}{\sum_{y_i\neq f(x_i)}W_i^{(t)}} {(\exp(\alpha_t) - \exp(-\alpha_t))}$。标黄的是什么呢？不就是 $e_t$ 吗！

所以优化问题最终的形式为

$$\min_{\alpha_t} \exp(-\alpha_t) + e_t(\exp(\alpha_t) - \exp(-\alpha_t))$$

求个导就可以解出 $\alpha_t$ 了：

$$-\exp(-\alpha_t) + e_t(\exp(\alpha_t) + \exp(-\alpha_t)) = 0$$

令 $\beta := \exp(-\alpha_t)$，

$$\begin{aligned} -\beta + \left( \frac{1}{\beta} + \beta \right)e_t &= 0 \\ \beta = \left( \frac{e_t}{1-e_t} \right)^{\frac{1}{2}} &= \exp(-\alpha_t)\\ \frac{1}{2}\log \frac{1-e_t}{e_t} &= \alpha_t\\ \end{aligned}$$

这就是我们为什么要将 $\alpha_t$ 这样赋值的原因。

回归问题

现在讨论一下回归问题。我们记得每一步的损失函数为

$$\sum_{i \in [n]}L(y_i, g_{t-1}(x_i) + \alpha_t f_t(x_i))$$

不过对于回归问题，我们不需要 $\alpha_t$，因为 $f_t$ 输出的是个实数，我们可以直接理解为 $\alpha_t$ 被吸收进了 $f_t$ 中，就没有必要优化两个东西了，只优化 $f_t$ 即可。

考虑使用平方损失函数，我们能推出什么样的模型。最优化问题为

$$\min_{f_t}\left( y_i - g_{t-1}(x_i) - f_t(x_i) \right)^{2}$$

令 $r_i^{(t)} := y_i - g_{t-1}(x_i)$，称为剩余误差（residual error），可以理解为之前的模型没能搞定的“剩余”的误差。所以其实就是，我们迭代地训练新模型 $f_t$ 来拟合 $\{(x_1,r_1^{(t)}), \cdots ,(x_n,r_n^{(t)})\}$。

此时，若 $f_t$ 为树模型，则这样的模型称为 Boosting Tree。

梯度提升模型（Gradient Boosting Model）

（一般而言使用树模型）

跟之前不同的是，此时不去拟合剩余误差了，而是拟合损失函数的负梯度，即

$$r_i^{(t)}:= - \frac{\partial L(y_i,\hat{y})}{\partial \hat{y}} \bigg|_{\hat{y} = g_{t-1}(x_i)}$$

即在模型预测值 $\hat{y}$（而非参数）的维度下做梯度下降，如图所示：

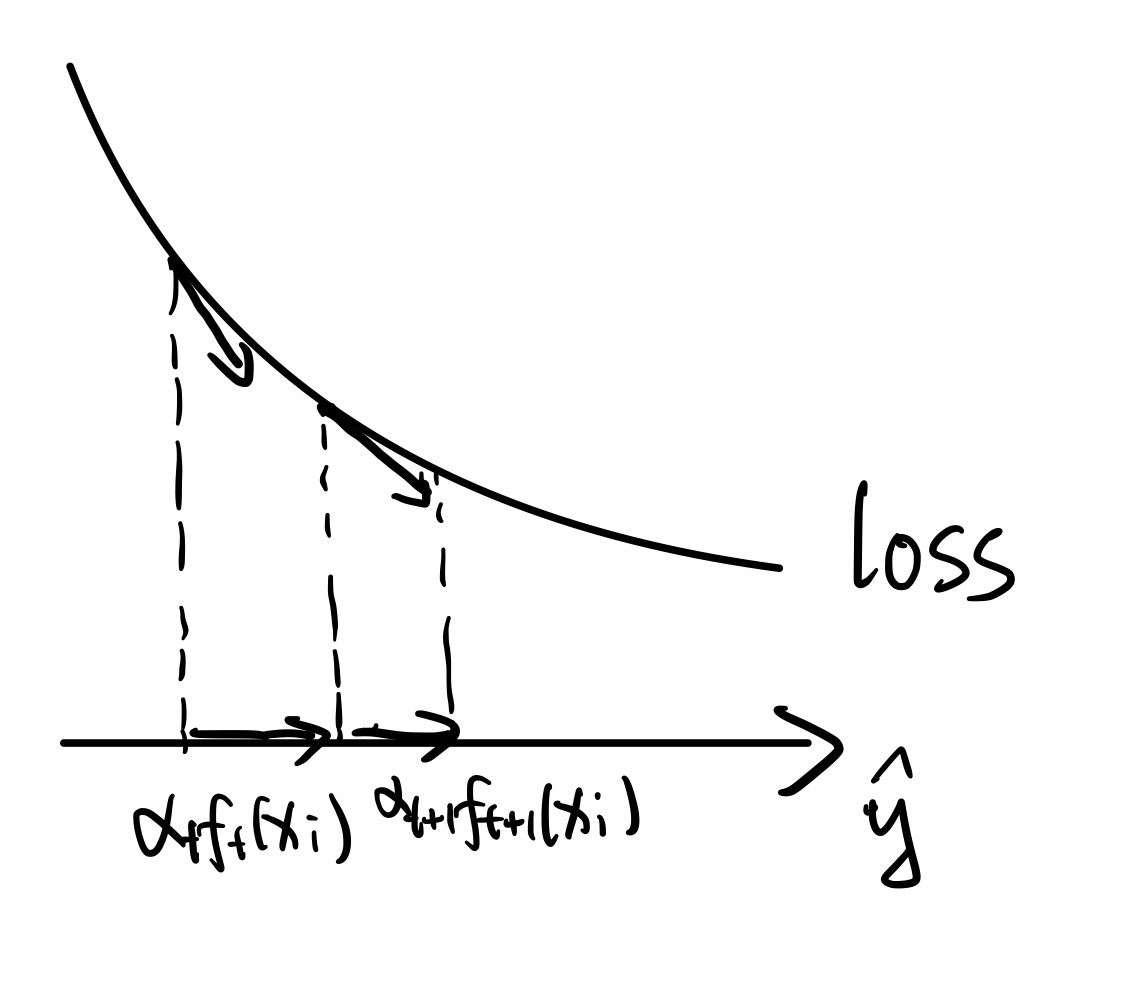
例如，对于平方损失函数 $\displaystyle L(y_i,\hat{y}) = \frac{1}{2}(y_i - \hat{y})^{2}$，其负梯度 $-\displaystyle \frac{\partial L(y_i,\hat{y})}{\partial \hat{y}} = y_i - \hat{y}$，其实就是之前提到的剩余误差，说明使用平方损失函数的情况下用梯度提升等价于拟合剩余误差。

介绍工业界模型 XGBoost：

进行二阶优化，对树模型复杂度的正则化，以及某些并行技术

很高效的模型。