线代 A1 笔记 第 13 部分（线性映射）

映射

具体的概念略，比如从 $S$ 到 $T$ 的映射 $f:S\to T$，$\alpha$ 映射到 $\beta$ 的话就是 $\alpha \mapsto \beta$。

$S$ 是定义域，$T$ 是陪域。$\beta$ 称为 $\alpha$ 的像，$\alpha$ 被称为 $\beta$ 的一个原像。$f$ 的像集记作 $\operatorname{Im} f$ 或 $f(S)$，又称值域。

注意值域与陪域的区别。$\operatorname{Im}f \subseteq T$。

• 单射：$\forall x_1,x_2\in S$，若 $x_1\neq x_2$ 则一定有 $f(x_1)\neq f(x_2)$。
• 满射：$f(S)=T$。即陪域中每个元素有至少一个原像。
• 双射/一一对应：陪域中每一个元素有唯一的一个原像。相当于即单又满。

每个元素都映射到自身的变换叫恒同变换，记作 $1_S$。$1_Tf = f 1_S$。

映射的乘法/合成：$f:S'\to S''$，$g:S\to S'$，（要求内层映射的陪域为外层映射的定义域），定义复合 $fg$。$(fg)(a)=f(g(a))$。

映射复合满足结合律：$f:S''\to S'''$，$g:S'\to S''$，$h:S\to S'$，则 $f(gh)=(fg)h$

• $f$ 有右逆等价于 $f$ 为满射。即 $f:S\to T$ 为满射 $\iff \exists g:T\to S$ s. t. $fg = 1_T$。（严格叙述需要选择公理）
• $f$ 有左逆等价于 $f$ 为单射。即 $f:S\to T$ 为单射 $\iff\exists g:T\to S$ s. t. $gf = 1_S$。

若 $f$ 有左逆和右逆，则称 $f$ 可逆，左逆和右逆唯一且相同。$f$ 可逆等价于 $f$ 为双射。

证明：必要性可以考虑证明 $f$ 为单射且 $f$ 为满射；充分性就直接从双射的定义出发。

必要性。设 $f: S\to T$ 可逆，则 $\exists f^{-1}:T\to S$，且 $ff^{-1} = 1_T$，$f^{-1}f=1_S$。$\forall a'\in T$，有 $f^{-1}(a')\in S$，且 $f(f^{-1}(a')) = (ff^{-1})(a')=a'=1_T(a')=a'$，故 $a'$ 在 $f$ 下总有一个原像 $f^{-1}(a')$，故 $f$ 为满射。

$\forall a_1,a_2\in S$，若 $f(a_1)=f(a_2)$，则 $f^{-1}(f(a_1))=f^{-1}(f(a_2))$，即 $1_S(a_1)=1_S(a_2)$，故 $a_1=a_2$，故 $f$ 为单射。从而 $f$ 为双射。

充分性。由 $f$ 为双射，$\forall a'\in T$，其在 $S$ 下有唯一原像 $a$，此时 $f(a)=a'$。令

$$\begin{aligned} g:T&\to S \\ a'&\mapsto a \end{aligned}$$

则 $(fg)(a') = f(g(a')) = f(a) = a'$，即 $fg = 1_T$。且 $\forall a\in S$，$g(f(a))=a$，即 $gf = 1_S$。故 $f$ 可逆。

线性映射

设 $\mathcal{A}: K^n\to K^m$，若 $\mathcal{A}$ 满足

• $\forall \alpha,\beta \in K^n$，有 $\mathcal{A}(\alpha+\beta)=\mathcal{A}(\alpha)+\mathcal{A}(\beta)$
• $\forall \alpha\in K^n,k\in K$，有 $\mathcal{A}(ka)=k \mathcal{A}(a)$

则称 $\mathcal{A}$ 为线性映射。$m=n$ 时称为 $K^n$ 上的线性变换。

线性映射可以保持向量组的线性相关性。例如：

• $\mathcal{A}(\boldsymbol{0}) = \boldsymbol{0}$
• $\mathcal{A}(k_1\alpha_1+ \cdots +k_s\alpha_s) = k_1 \mathcal{A}(\alpha_1) + \cdots + k_s \mathcal{A}(\alpha_s)$。
• 若 $\alpha_1, \cdots ,\alpha_s$ 线性相关，则 $\mathcal{A}(\alpha_1), \cdots ,\mathcal{A}(\alpha_s)$ 也线性相关。
• 反之一般不成立（理解：线性映射是秩不升的）

基底的像确定线性映射：若 $\alpha_1, \cdots ,\alpha_n$ 为 $K^n$ 的一组基，在 $K^m$ 中指定任意 $n$ 个向量 $\beta_1, \cdots ,\beta_n$，则存在唯一的线性映射 $\mathcal{A}:K^n\to K^m$ s. t. $\forall 1\le i\le n$ 有 $\mathcal{A}(\alpha_i) = \beta_i$。

如何理解？考虑 $K^n$ 中每一个元素都可以写成 $k_1\alpha_1+k_2\alpha_2+ \cdots +k_n\alpha_n$ 的形式，我们定义线性映射

$$\begin{aligned} \mathcal{A}: K^n&\longrightarrow K^m\\ k_1\alpha_1+ \cdots +k_n\alpha_n &\longmapsto k_1\beta_1+ \cdots +k_n\beta_n\\ \end{aligned}$$

其中 $k_1, \cdots k_n\in K$。容易证明其为线性映射。存在性证毕。

唯一性也是显然的。根据我们如上的定义，对于 $\forall \alpha\in K^n$，其都能被唯一写成 $k_1\alpha_1+ \cdots +k_n\alpha_n$ 的形式，由线性映射的性质，$\mathcal{A}$ 若存在则一定唯一。

两个子空间

• 像空间：不难验证 $\operatorname{Im} \mathcal{A}$ 为 $K^m$ 的子空间。称为 $\mathcal{A}$ 的像空间。
• 核空间：$\operatorname{Ker} \mathcal{A} := \left\{ \alpha\in K^n \mid \mathcal{A} \alpha = 0 \right\}$ 为 $K^n$ 的子空间（同样不难验证），称为 $\mathcal{A}$ 的核空间。

两个基本事实。设 $A\in M_{m\times n}(K)$，令

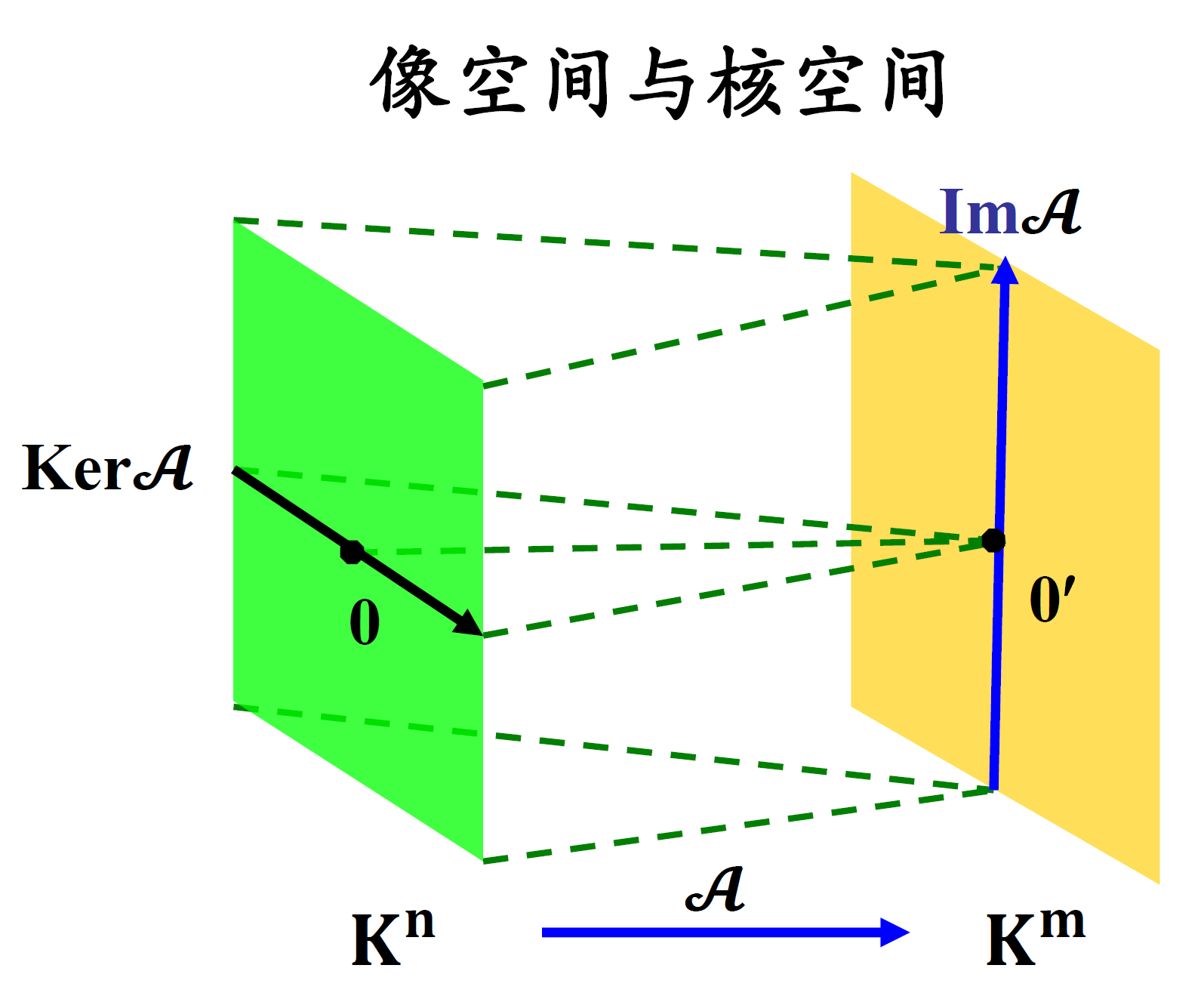
$$\begin{aligned} \mathcal{A}:K^n&\longrightarrow K^m \\ \alpha&\longmapsto A\alpha \end{aligned}$$

不难发现 $\mathcal{A}$ 为线性映射。

• 设 $A$ 的列向量组为 $\alpha_1, \cdots ,\alpha_n$，则 $\operatorname{Im} \mathcal{A} = \mathcal{C}(A)$。
• $\operatorname{Ker} \mathcal{A} = \mathcal{N}(A)$。

所以 $\operatorname{dim}(\operatorname{Ker} \mathcal{A}) + \operatorname{dim}(\operatorname{Im} \mathcal{A}) = n$。